题目内容
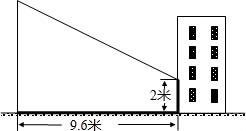 赵亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,旗杆的地面部分影长BC=9.6米,另一部分影长落在某一建筑的墙EC=2米上,求学校旗杆的高度.
赵亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,旗杆的地面部分影长BC=9.6米,另一部分影长落在某一建筑的墙EC=2米上,求学校旗杆的高度.
分析:做DE⊥AB于D,可得矩形BCED,利用同一时刻物高与影长的比一定得到AD的长度,加上CE的长度即为旗杆的高度.
解答: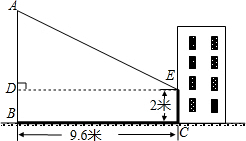 解:DE⊥AB于D,
解:DE⊥AB于D,
∵DB⊥BC于B,EC⊥BC于C,
∴四边形BCED为矩形.
∴DE=BC=9.6m,BD=EC=2m,
∵同一时刻物高与影长所组成的三角形相似,
∴
=
,
解得AD=8m.
∴AB=8+2=10m.
答:旗杆的高度为10m.
 解:DE⊥AB于D,
解:DE⊥AB于D,∵DB⊥BC于B,EC⊥BC于C,
∴四边形BCED为矩形.
∴DE=BC=9.6m,BD=EC=2m,
∵同一时刻物高与影长所组成的三角形相似,
∴
| 1 |
| 1.2 |
| AD |
| 9.6 |
解得AD=8m.
∴AB=8+2=10m.
答:旗杆的高度为10m.
点评:考查相似三角形的应用;构造出直角三角形进行求解是解决本题的难点;用到的知识点为:同一时刻物高与影长的比一定.

练习册系列答案
相关题目
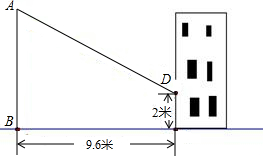 赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,求学校旗杆的高度.
赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,求学校旗杆的高度.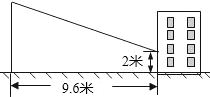 赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为
赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为
