题目内容
画线段MN=3㎝,在线段MN上取一点Q,使MQ=NQ,延长线段MN至点A,使AN=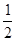 MN;延长线段NM至点B,使BN=3BM,根据所画图形计算:
MN;延长线段NM至点B,使BN=3BM,根据所画图形计算:
(1)线段BM的长度;
(2)线段AN的长度;
(3)试说明Q是哪些线段的中点?图中共有多少条线段?它们分别是?
【答案】
(1)1.5㎝;(2)1.5㎝;(3)由图可知,BM=MQ=NQ=NA
所以Q既是线段MN的中点,也是线段AB的中点。
图中共有10条线段,它们分别是:BM、BQ、BN、BA、MQ、MN、MA、QN、QA、NA.
【解析】
试题分析:先根据题意画出几何图形
(1)根据BN=3BM可得到MN=2BM,而MN=3cm,即可得到线段BM的长;
(2)根据AN=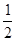 MN即可得到线段AN的长;
MN即可得到线段AN的长;
(3)由(1)与(2)得到BM=MQ=NQ=NA,即QB=QA,QM=QN,则点Q是线段MN的中点,也是线段AB的中点;图形中共有BM、BQ、BN、BA、MQ、MN、MA、QN、QA、NA10条线段.
如图所示:

(1)∵MN=3cm,BN=3BM,
∴BM=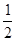 MN=
MN=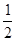 ×3=1.5(cm );
×3=1.5(cm );
(2)∵MN=3cm,AN=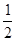 MN
MN
∴AN=1.5cm;
(3)由图可知,BM=MQ=NQ=NA,
∴QB=QA,QM=QN,
∴点Q既是线段MN的中点,也是线段AB的中点;
图中共有10条线段,它们分别是:BM、BQ、BN、BA、MQ、MN、MA、QN、QA、NA.
考点:两点间的距离、射线与线段的定义
点评:解题的关键是熟记两点间的距离的定义:两点的连线段的长叫两点间的距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
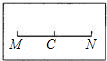 如图所示,七年级(2)班的孟飞同学在一张透明纸上画了一条长8厘米的线段MN,并在线段MN上任意找了一个不同于M,N的点C,然后用折纸的方法找出了线段MC,NC的中点A,B,并求出了线段AB的长,想一想,孟飞是如何找到线段MC,NC的中点的,又是如何求出线段AB的长度的?
如图所示,七年级(2)班的孟飞同学在一张透明纸上画了一条长8厘米的线段MN,并在线段MN上任意找了一个不同于M,N的点C,然后用折纸的方法找出了线段MC,NC的中点A,B,并求出了线段AB的长,想一想,孟飞是如何找到线段MC,NC的中点的,又是如何求出线段AB的长度的?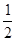 MN;延长线段NM至点B,使BN=3BM,根据所画图形计算:
MN;延长线段NM至点B,使BN=3BM,根据所画图形计算:  MN;延长线段NM至点B,使BN=3BM,根据所画图形计算:
MN;延长线段NM至点B,使BN=3BM,根据所画图形计算: