题目内容
(2013•呼和浩特)在平面直角坐标系中,已知点A(4,0)、B(-6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为
(0,12)或(0,-12)
(0,12)或(0,-12)
.分析:如解答图所示,构造含有90°圆心角的⊙P,则⊙P与y轴的交点即为所求的点C.
注意点C有两个.
注意点C有两个.
解答: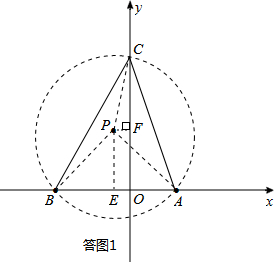 解:设线段BA的中点为E,
解:设线段BA的中点为E,
∵点A(4,0)、B(-6,0),∴AB=10,E(-1,0).
(1)如答图1所示,过点E在第二象限作EP⊥BA,且EP=
AB=5,则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5
;
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=
∠BPA=45°,即则点C即为所求.
过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,
在Rt△PFC中,PF=1,PC=5
,由勾股定理得:CF=
=7,
∴OC=OF+CF=5+7=12,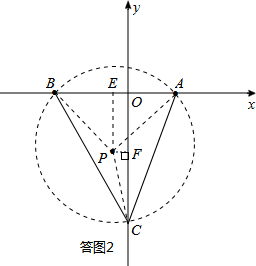
∴点C坐标为(0,12);
(2)如答图2所示,在第3象限可以参照(1)作同样操作,同理求得y轴负半轴上的点C坐标为(0,-12).
综上所述,点C坐标为(0,12)或(0,-12).
故答案为:(0,12)或(0,-12).
 解:设线段BA的中点为E,
解:设线段BA的中点为E,∵点A(4,0)、B(-6,0),∴AB=10,E(-1,0).
(1)如答图1所示,过点E在第二象限作EP⊥BA,且EP=
| 1 |
| 2 |
| 2 |
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=
| 1 |
| 2 |
过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,
在Rt△PFC中,PF=1,PC=5
| 2 |
| PC2-PF2 |
∴OC=OF+CF=5+7=12,

∴点C坐标为(0,12);
(2)如答图2所示,在第3象限可以参照(1)作同样操作,同理求得y轴负半轴上的点C坐标为(0,-12).
综上所述,点C坐标为(0,12)或(0,-12).
故答案为:(0,12)或(0,-12).
点评:本题难度较大.由45°的圆周角联想到90°的圆心角是解题的突破口,也是本题的难点所在.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
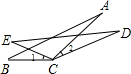 (2013•呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
(2013•呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.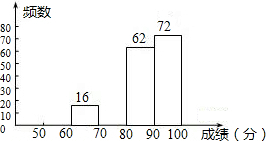 (2013•呼和浩特)某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分进行统计.
(2013•呼和浩特)某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分进行统计.