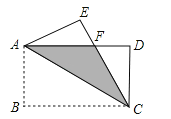
题目内容
【题目】如图，△ABC中，AC=BC，∠ACB=120°，点D在AB边上运动（D不与A、B重合），连结CD．作∠CDE=30°，DE交AC于点E．
（1）当DE∥BC时，△ACD的形状按角分类是 ；
在点D的运动过程中，△ECD的形状可以是等腰三角形吗？若可以，请求出∠AED的度数；若不可以，请说明理由．
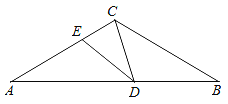
【答案】（1）直角三角形；（2）可以是等腰三角形，∠AED度数为60°或105°.
【解析】试题分析：（1）由DE∥BC得到∠BCD=∠CDE=30°，再由∠ACB=120°，得到∠ACD=120°﹣30°=90°，则△ACD是直角三角形．
（2）分类讨论：当∠CDE=∠ECD时，EC=DE；当∠ECD=∠CED时，CD=DE；当∠CED=∠CDE时，EC=CD；然后利用等腰三角形的性质和三角形的内角和定理进行计算．
试题解析：解：（1）∵△ABC中，AC=BC，∴∠A=∠B=（180°-∠ACB）÷2=（180°-120°）÷2=30°．∵DE∥BC，∴∠ADE=∠B=30°．又∵∠CDE=30°，∴∠ADC=∠ADE+∠CDE=30°+30°=60°，∴∠ACD=180°﹣∠A﹣∠ADC=180°﹣30°﹣60°=90°，∴△ACD是直角三角形；
（2）△ECD可以是等腰三角形．理由如下：
①当∠CDE=∠ECD时，EC=DE，∴∠ECD=∠CDE=30°，∵∠AED=∠ECD+∠CDE，∴∠AED=60°；
②当∠ECD=∠CED时，CD=DE，∵∠ECD+∠CED+∠CDE=180°，∴∠CED=（180°-∠CDE）÷2=（180°-30°）÷2=75°，∴∠AED=180°﹣∠CED=105°；
③当∠CED=∠CDE时，EC=CD，∠ACD=180°﹣∠CED﹣∠CDE=180°﹣30°﹣30°=120°，∵∠ACB=120°，∴此时，点D与点B重合，不合题意．
综上所述：△ECD可以是等腰三角形，此时∠AED的度数为60°或105．
