题目内容
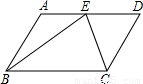
(2007•天水)已知:如图,在?ABCD中,点E在AD上,BE,CE分别是∠ABC,∠BCD的角平分线.求证:BC=2AB.
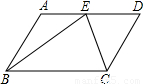
【答案】分析:主要是得出AB=AE,CD=DE,也就是证,∠ABE=∠AEB,∠DEC=∠ECD,那么可以利用角平行性质和平行四边形的性质,等量代换可得到两组角相等,而AB=CD,所以可以得出结论.
解答:证明:∵BE,CE分别是∠ABC,∠BCD的角平分线,
∴∠ABE=∠EBC,∠BCE=∠ECD.
又∵ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠EBC,∠DEC=∠BCE.
∴∠ABE=∠AEB,∠DEC=∠ECD.
∴AB=AE,CD=DE.
又四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∴BC=AD=AE+DE=AB+CD=2AB.
点评:本题利用角平行性质和平行四边形的性质(平行四边形的对边分别平行且相等).
解答:证明:∵BE,CE分别是∠ABC,∠BCD的角平分线,
∴∠ABE=∠EBC,∠BCE=∠ECD.
又∵ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠EBC,∠DEC=∠BCE.
∴∠ABE=∠AEB,∠DEC=∠ECD.
∴AB=AE,CD=DE.
又四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∴BC=AD=AE+DE=AB+CD=2AB.
点评:本题利用角平行性质和平行四边形的性质(平行四边形的对边分别平行且相等).

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目