题目内容
【题目】如图,在平面直角坐标系xoy中,⊙O的圆心O在坐标原点,半径OB在x轴正半轴上,点P是⊙O外一点,连接PO,与⊙O交于点A,PC、PD是⊙O的切线,切点分别为点C、点D,AO=OB=2,∠POB=120°,点M 坐标为(1,-![]() ).
).
(1)求证:OP⊥CD;
(2)连结OM,求∠AOM的大小;
(3) 如果点E在x轴上,且△ABE与△AOM相似,求点E的坐标.
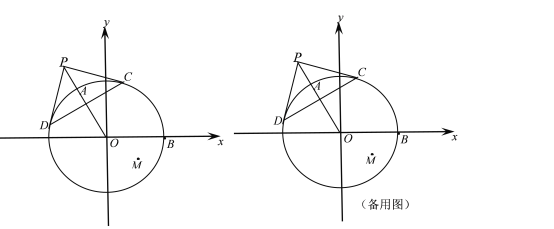
【答案】(1)见解析;(2)150°;(3) E(4,0)或(8,0).
【解析】
(1)根据直线与圆相切的性质证明Rt△PDO ≌Rt△PCO,就可以证明OP⊥CD(2)连接OM,利用三角函数值解直角三角形即可(3)根据△ABE与△AOM相似,可以得到边,角的关系,进而得到点的坐标.
(1)连接OD、OC
∵PC、PD是⊙O的切线
∴∠PDO=∠PCO=90° ,PC=PD
∵在Rt△PDO 与Rt△PCO中
![]() ∴Rt△PDO ≌Rt△PCO(HL)
∴Rt△PDO ≌Rt△PCO(HL)
∴∠CPO=∠DPO
∵PC=PD,∠CPO=∠DPO
∴OP⊥CD
(2)连接OM,作MH⊥x轴
∵在Rt△HMO中 ∴tan∠HOM=![]() =
=![]() ∴ ∠HOM=30°
∴ ∠HOM=30°
∴ ∠AOM=∠HOM+∠POB=30°+120°=150°
(3)由OA=OB=2,∠AOB=120°,得∠ABO=30°
若点E在点B左侧时,不论∠AEB和∠EAB哪个
角等于150°,此时三角形内角和都大于180°
则点E只能在点B右侧
∵∠ABO=30°∴∠ABE=∠AOM=150°
若△ABE与△AOM相似存在两种情况
①△AOM ∽△ABE ∴![]() =
=![]()
∴ BE=2
∴E(4,0)
②△AOM ∽△EBA ∴![]() =
=![]()
∴ BE=6
∴E(8,0)
综上所述:E(4,0)或(8,0).

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.