题目内容
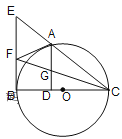
【题目】如图,A是以BC为直径的⊙O上的一点, AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E, 点F是EB的中点,连结CF交AD于点G.
(1)求证:AF是⊙O的切线;
(2)求证:AG=GD;
(3)若FB=FG,且⊙O的半径长为![]() ,求BD.
,求BD.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
试题分析:(1)连接AB, OA,根据直径所对的圆周角是直角可得∠BAC=90°,∠BAE=90°,根据切线的判定与性质可证明;
(2)利用相似三角形的性质与判定可证明;
(3)过点F作FH⊥AD于点H,由等腰三角形和相似三角形的性质与判定可求解.
试题解析:(1)连接AB, OA,
∵BC是直径
∴∠BAC=90°,∠BAE=90°
∵点F是EB的中点
∴AF=BF=EF
∵AF=BF
∴∠FBA=∠FAB
∵OB=OA
∴∠OBA=∠OAB
∴∠FBD=∠FAO
∵BF是⊙O的切线
∴∠FBD=90°
∴∠FAO=90°
∴AF是⊙O的切线。
(2)∵AD⊥BC,∠FBD=90°
∴EB∥AD
∴△FBC∽△GDC, △EBC∽△ADC
∴![]() ,
,![]()
∴![]()
∵EF=FB
∴AG=GD
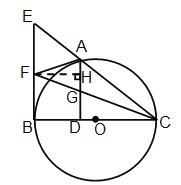
(3)过点F作FH⊥AD于点H
∵AD⊥BC, FH⊥AD
∴FH∥BC
∴∠FHG=∠GDO, ∠HFG=∠DCG
∴△HFG∽△DCG
∵AD⊥BC, FH⊥AD,EB⊥BC
∴四边形HFBD是矩形
∴FH=BD
∵FG=FB,FB=FA
∴FA=FG
∴△AFG是等腰三角形
∴![]() ,
,
∵AG=GD
∴![]()
设BD=x,则FH=x,CD=![]()
∵△HFG∽△DCG
∴![]()
∴![]()
![]()
∴BD=![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目