题目内容
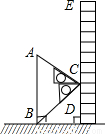
如图，为了测量某建筑物AB的高度，小亮在教学楼DE的三楼找到一个观测点C，利用三角板测得建筑物AB顶端A点的仰角为30°，底部B点的俯角为45°．若CD=9米，求建筑物AB的高度（结果精确到0.1米，参考数据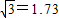
）．
【答案】分析：首先分析图形，根据题意构造直角三角形．本题涉及多个直角三角形，应利用其公共边构造关系式求解．
解答：
解：过点C作CF⊥AB于F．
∵∠BCF=∠CBD=45°，CD=9，
∴CF=BD=CD=BF=9
在Rt△AFC中，
∵∠AEC=90°，∠ACF=30°，
∴AF=tan∠ACF•FC=9×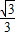
=3
，
∴AB=AF+BF=3
+9≈14.2（米）．
所以，建筑物AB的高度约14.2米．
点评：考查了解直角三角形的应用-仰角俯角问题，本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．
解答：
解：过点C作CF⊥AB于F．∵∠BCF=∠CBD=45°，CD=9，
∴CF=BD=CD=BF=9
在Rt△AFC中，
∵∠AEC=90°，∠ACF=30°，
∴AF=tan∠ACF•FC=9×
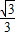=3，∴AB=AF+BF=3
+9≈14.2（米）．所以，建筑物AB的高度约14.2米．
点评：考查了解直角三角形的应用-仰角俯角问题，本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
如图，某数学活动小组为了测量我市文化广场的标志建筑“太阳鸟”的高度AB，在D处用高1.2米的测角仪CD，测得最高点A的仰角为32.6°，再向“太阳鸟”的方向前进20米至D′处，测得最高点A的仰角为45°，点D、D′、B在同一条直线上．求“太阳鸟”的高度AB．（精确到0.1米）