题目内容
如图，在反比例函数的图象上有不重合的两点A、B，且A点的坐标是（4，2），B点的横坐标为2，BB1和AA1都垂直于x轴，垂足分别为B1和A1．（1）求B点纵坐标；（2）求S△OBA．
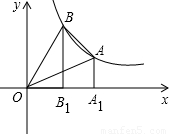
【答案】分析：（1）首先用待定系数法求得反比例函数的解析式，然后进一步求得点B的坐标；
（2）结合图形和反比例函数可知要求的三角形的面积就是梯形的面积．
解答：解：（1）设反比例函数是y=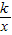
，
把x=4，y=2代入得k=8．
则反比例函数解析式是y=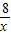
，
当x=2时，则y=4．即点B的纵坐标是4．
（2）根据反比例函数的解析式，知三角形OAA1的面积和三角形OBB1的面积相等，都是4，
则要求的三角形的面积等于直角梯形ABB1A1的面积是
×（2+4）×2=6．
点评：要能够熟练运用待定系数法求得反比例函数的解析式；双曲线上任意一点向x轴或y轴引垂线，则该点、垂足、原点组成的三角形的面积相等，都是
．
（2）结合图形和反比例函数可知要求的三角形的面积就是梯形的面积．
解答：解：（1）设反比例函数是y=
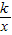，把x=4，y=2代入得k=8．
则反比例函数解析式是y=
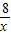，当x=2时，则y=4．即点B的纵坐标是4．
（2）根据反比例函数的解析式，知三角形OAA1的面积和三角形OBB1的面积相等，都是4，
则要求的三角形的面积等于直角梯形ABB1A1的面积是
×（2+4）×2=6．点评：要能够熟练运用待定系数法求得反比例函数的解析式；双曲线上任意一点向x轴或y轴引垂线，则该点、垂足、原点组成的三角形的面积相等，都是
． 
练习册系列答案
阅读快车系列答案
相关题目
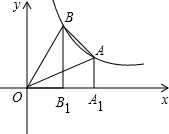如图，在反比例函数的图象上有不重合的两点A、B，且A点的坐标是（4，2），B点的横坐标为2，BB1和AA1都垂直于x轴，垂足分别为B1和A1．
的图象上，有点
，
，
，
，它们的横坐标依次为1，2，3，4
.分别过这些点作
轴与
轴的垂线，图中所构成的阴影部分的面积从左到右依次为
，
，
，求：
的值；
的值。（用含
的代数式来表示）
的图象上任取一点P，过P点分别作x轴，y轴的垂线，垂足分别为M，N，那么四边形PMON的面积为 ．
的图象上，有点
，
，
，
，它们的横坐标依次为1，2，3，4
.分别过这些点作
轴与
轴的垂线，图中所构成的阴影部分的面积从左到右依次为
，
，
，求：
的值；
的值。（用含
的代数式来表示）