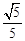题目内容
已知:如图,在△ABC中,CD⊥AB,sinA= ,AB=13,CD=12,求AD的长和tanB的值.
,AB=13,CD=12,求AD的长和tanB的值.
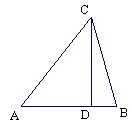
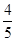 ,AB=13,CD=12,求AD的长和tanB的值.
,AB=13,CD=12,求AD的长和tanB的值.
解:∵CD⊥AB,
∴∠CDA=90°
∵ sinA=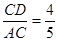
∴ AC=15
∴AD=9.
∴BD="4."
∴tanB=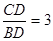
∴∠CDA=90°
∵ sinA=
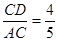
∴ AC=15
∴AD=9.
∴BD="4."
∴tanB=
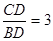
由sinA=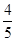 ,CD=12,根据三角函数可得AC=15,根据勾股定理可得AD=9,则BD=4,再根据正切的定义求出tanB的值.
,CD=12,根据三角函数可得AC=15,根据勾股定理可得AD=9,则BD=4,再根据正切的定义求出tanB的值.
 ,CD=12,根据三角函数可得AC=15,根据勾股定理可得AD=9,则BD=4,再根据正切的定义求出tanB的值.
,CD=12,根据三角函数可得AC=15,根据勾股定理可得AD=9,则BD=4,再根据正切的定义求出tanB的值.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 三等分,连接PC并延长PC交y轴于点D(0,3).
三等分,连接PC并延长PC交y轴于点D(0,3).
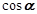 的值是( )
的值是( )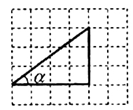
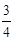
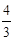
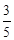
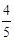
 中,
中,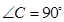 ,
, ,
, ,将△
,将△ 旋转后点
旋转后点 落在直线
落在直线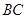 上的点
上的点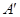 ,点
,点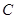 落在点
落在点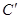 处,那么
处,那么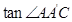 的值是 .
的值是 .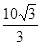 米
米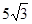 米
米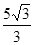 米
米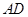 ∥
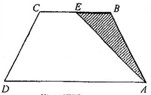
∥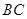 ,坝高10m,迎水坡面
,坝高10m,迎水坡面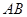 的坡度
的坡度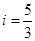 ,审核组专家看后,从力学的角度对此方案提出了建议,李设计师决定在原方案的基础上,将迎水坡面
,审核组专家看后,从力学的角度对此方案提出了建议,李设计师决定在原方案的基础上,将迎水坡面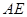 的坡度
的坡度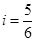 .
.
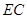 方向拓宽
方向拓宽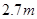 ,求坝底将会沿
,求坝底将会沿