题目内容
如图,矩形木块ABCD放置在直线L上,将其向右作无滑动的翻滚,直到被正方形PQRS挡住为止,已知AB=3,BC=4,BP=16,正方形木块PQRS边长为2| 3 |

分析:点D翻滚时,走过的路径长是三段弧的弧长,第一次的旋转是以C为圆心,CD为半径,旋转的角度是90度;第二次旋转是以点D为圆心,没有路程;第三次是以A为圆心,AD为半径,旋转的角度是90度;第四次是以点B为圆心,BD为半径,角度是30度.所以根据弧长公式可得.
解答:解:第一次旋转是以点C为圆心,CD为半径,旋转角度是90度,
所以弧长=
=1.5π;
第二次旋转是以点D为圆心,所以没有路程;
第三次旋转是以点A为圆心,AD为半径,角度是90度,
所以弧长=
=2π;
第四次是以点B为圆心,BD为半径,角度是30度,
所以弧长=
=
π;
所以点D经过的路线为=1.5π+2π+
π=
π.
故答案为:
π.
所以弧长=
| 90π×3 |
| 180 |
第二次旋转是以点D为圆心,所以没有路程;
第三次旋转是以点A为圆心,AD为半径,角度是90度,
所以弧长=
| 90π×4 |
| 180 |
第四次是以点B为圆心,BD为半径,角度是30度,
所以弧长=
30π×
| ||
| 180 |
| 5 |
| 6 |
所以点D经过的路线为=1.5π+2π+
| 5 |
| 6 |
| 13 |
| 3 |
故答案为:
| 13 |
| 3 |
点评:考查了弧长的计算,矩形的性质和勾股定理,本题的关键是弄清弧长的半径及圆心,圆心角的度数.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,则折痕DG的长为( )
如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,则折痕DG的长为( ) MN折叠,使MB与DN交于点K,得到△MNK,则对△MNK的叙述正确的个数是:( )
MN折叠,使MB与DN交于点K,得到△MNK,则对△MNK的叙述正确的个数是:( ) ,则点D经过的路线为________.
,则点D经过的路线为________.
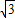 ,则点D经过的路线为 .
,则点D经过的路线为 .