题目内容
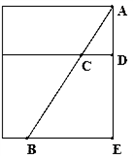
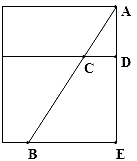
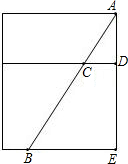 如图,一油桶高AE为1m,桶内有油,一根木棒AB长为1.2m,从桶盖的小口(A)处斜插入桶内,一端插到桶底,另一端与小口(A)齐平,抽出木棒,量得棒上未浸油部分AC长为0.48m.求桶内油面的高度DE.
如图,一油桶高AE为1m,桶内有油,一根木棒AB长为1.2m,从桶盖的小口(A)处斜插入桶内,一端插到桶底,另一端与小口(A)齐平,抽出木棒,量得棒上未浸油部分AC长为0.48m.求桶内油面的高度DE.
解:∵CD∥BE,
∴△ACD∽△ABE,
∴ =
= ,
,
∴ =
= ,
,
∴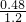 =
=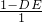 ,
,
解得:DE=0.6m.
分析:因为油面与桶底平行,所以△ACD∽△ABE,根据相似三角形的性质即可求出油面高DE的长度.
点评:本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
∴△ACD∽△ABE,
∴
 =
= ,
,∴
 =
= ,
,∴
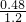 =
=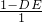 ,
,解得:DE=0.6m.
分析:因为油面与桶底平行,所以△ACD∽△ABE,根据相似三角形的性质即可求出油面高DE的长度.
点评:本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
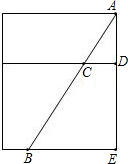 如图,一油桶高AE为1m,桶内有油,一根木棒AB长为1.2m,从桶盖的小口(A)处斜插入桶内,一端插到桶底,另一端与小口(A)齐平,抽出木棒,量得棒上未浸油部分AC长为0.48m.求桶内油面的高度DE.
如图,一油桶高AE为1m,桶内有油,一根木棒AB长为1.2m,从桶盖的小口(A)处斜插入桶内,一端插到桶底,另一端与小口(A)齐平,抽出木棒,量得棒上未浸油部分AC长为0.48m.求桶内油面的高度DE.