题目内容
若a、b 是正数，a-b=l，ab=2，则a+b=（ ）
| A．-3 | B．3 | C．±3 | D．9 |
B
分析：根据（a+b）2=（a-b）2+4ab，代值计算，再开平方求解．注意若a、b 是正数，则a+b＞0．
解答：解：∵（a+b）2=（a-b）2+4ab=12+4×2=9，
开平方，得a+b=±3，
又∵a、b 是正数，
∴a+b＞0，
∴a+b=3．
故选B．
解答：解：∵（a+b）2=（a-b）2+4ab=12+4×2=9，
开平方，得a+b=±3，
又∵a、b 是正数，
∴a+b＞0，
∴a+b=3．
故选B．
练习册系列答案
口算题天天练系列答案
相关题目
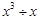的结果是 （ ）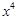
.
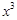
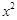
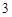
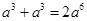
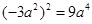
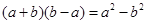
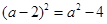
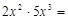