题目内容
已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数y=kx+1的图象与二次函数的图象交于A,B两点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.(1)求一次函数与二次函数的解析式;
(2)判断以线段AB为直径的圆与直线l的位置关系,并给出证明;
(3)把二次函数的图象向右平移2个单位,再向下平移t个单位(t>0),二次函数的图象与x轴交于M,N两点,一次函数图象交y轴于F点.当t为何值时,过F,M,N三点的圆的面积最小?最小面积是多少?
【答案】分析:(1)设二次函数的解析式是y=ax2,把A(-4,4)代入求出a代入一次函数求出k,即可得到答案;
(2)求出B、O的坐标,求出OA和O到直线y=-1的距离即可得出答案;
(3)作MN的垂直平分线,△FMN外接圆的圆心O在直线上,求出MN、DN,根据勾股定理求出O'F=O'N的圆心坐标的纵坐标Y,求出y取何值时r最小,即可求出答案.
解答:解:(1)设二次函数的解析式是y=ax2(a≠0),
把A(-4,4)代入得:4=16a,
a= ,
,
∴y= x2,
x2,
把A(-4,4)代入y=kx+1得:4=-4k+1,
∴k=- ,
,
∴y=- x+1,
x+1,
答:一次函数与二次函数的解析式分别为y=- x+1,y=
x+1,y= x2.
x2.
(2)答:以线段AB为直径的圆与直线l的位置关系是相切.
证明: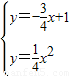 得:
得: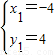 ,
,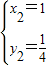 ,
,
∴B(1, ),
),
AB的中点O的坐标是(- ,
,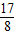 ),
),
OA=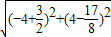 =
=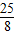 ,
,
O到直线y=-1的距离是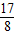 +1=
+1= =0B,
=0B,
∴以线段AB为直径的圆与直线l的位置关系是相切.
(3)解:作MN的垂直平分线,△FMN外接圆的圆心O在直线上,
由于平移后的抛物线对称轴为x=2,对称轴交x轴于D,
F(0,1)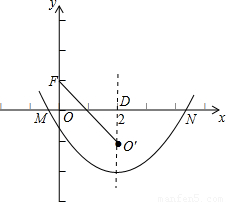 ,平移后二次函数的解析式是y=
,平移后二次函数的解析式是y= (x-2)2-t,即y=
(x-2)2-t,即y= x2-x+1-t,
x2-x+1-t,
当y=0时, x2-x+1-t=0,
x2-x+1-t=0,
设M(e,0),N(f,0),N在M的右边,
则e+f=-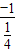 =4,e•f=
=4,e•f=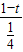 =4-4t,
=4-4t,
∴MN=f-e=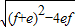 =4
=4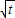 ,
,
MD=2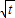 ,
,
设圆心坐标(2,y),根据OF=ON,
∴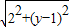 =
=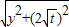 ,
,
y= -2t,
-2t,
r=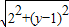 =
=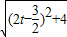 ,
,
当t= 时,半径有最小值2,圆面积最小为4π,
时,半径有最小值2,圆面积最小为4π,
答:当t为 时,过F,M,N三点的圆的面积最小,最小面积是4π.
时,过F,M,N三点的圆的面积最小,最小面积是4π.
点评:本题主要考查对用待定系数法求二次函数、一次函数的解析式,勾股定理,二次函数的最值,直线与圆的位置关系,解二元二次方程组等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.
(2)求出B、O的坐标,求出OA和O到直线y=-1的距离即可得出答案;
(3)作MN的垂直平分线,△FMN外接圆的圆心O在直线上,求出MN、DN,根据勾股定理求出O'F=O'N的圆心坐标的纵坐标Y,求出y取何值时r最小,即可求出答案.
解答:解:(1)设二次函数的解析式是y=ax2(a≠0),
把A(-4,4)代入得:4=16a,
a=
 ,
,∴y=
 x2,
x2,把A(-4,4)代入y=kx+1得:4=-4k+1,
∴k=-
 ,
,∴y=-
 x+1,
x+1,答:一次函数与二次函数的解析式分别为y=-
 x+1,y=
x+1,y= x2.
x2.(2)答:以线段AB为直径的圆与直线l的位置关系是相切.
证明:
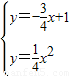 得:
得: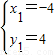 ,
,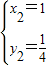 ,
,∴B(1,
 ),
),AB的中点O的坐标是(-
 ,
,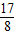 ),
),OA=
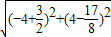 =
=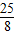 ,
,O到直线y=-1的距离是
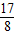 +1=
+1= =0B,
=0B,∴以线段AB为直径的圆与直线l的位置关系是相切.
(3)解:作MN的垂直平分线,△FMN外接圆的圆心O在直线上,
由于平移后的抛物线对称轴为x=2,对称轴交x轴于D,
F(0,1)
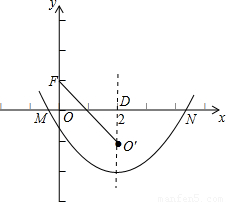 ,平移后二次函数的解析式是y=
,平移后二次函数的解析式是y= (x-2)2-t,即y=
(x-2)2-t,即y= x2-x+1-t,
x2-x+1-t,当y=0时,
 x2-x+1-t=0,
x2-x+1-t=0,设M(e,0),N(f,0),N在M的右边,
则e+f=-
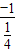 =4,e•f=
=4,e•f=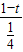 =4-4t,
=4-4t,∴MN=f-e=
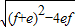 =4
=4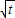 ,
,MD=2
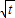 ,
,设圆心坐标(2,y),根据OF=ON,
∴
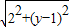 =
=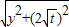 ,
,y=
 -2t,
-2t,r=
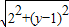 =
=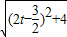 ,
,当t=
 时,半径有最小值2,圆面积最小为4π,
时,半径有最小值2,圆面积最小为4π,答:当t为
 时,过F,M,N三点的圆的面积最小,最小面积是4π.
时,过F,M,N三点的圆的面积最小,最小面积是4π.点评:本题主要考查对用待定系数法求二次函数、一次函数的解析式,勾股定理,二次函数的最值,直线与圆的位置关系,解二元二次方程组等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 ,且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
,且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点. 点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.