Question

（本小题满分12分）

如图，在直角梯形ABCD中，AD∥BC，，AD = 6，BC = 8，，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．设点P，Q运动的时间是t秒(t＞0)．

 

 

 

 

 

 

 

1.（1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．

2.（2）当BP = 1时，求△EPQ与梯形ABCD重叠部分的面积．

3.（3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．

 

Answer 1

 

1.（1）y = 2t

2.（2）当BP = 1时，有两种情形：

①如图6，若点P从点M向点B运动，有 MB = = 4，MP = MQ= 3，

∴PQ = 6．连接EM，

∵△EPQ是等边三角形，∴EM⊥PQ．∴．

∵AB = ，∴点E在AD上．

∴△EPQ与梯形ABCD重叠部分就是△EPQ，其面

积为．

②若点P从点B向点M运动，由题意得 ．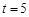

PQ = BM + MQBP = 8，PC = 7．设PE与AD交于点F，QE与AD或AD的

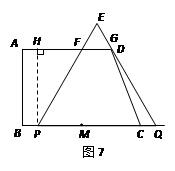延长线交于点G，过点P作PH⊥AD于点H，则

HP = ，AH = 1．在Rt△HPF中，∠HPF = 30°，

∴HF = 3，PF = 6．∴FG = FE = 2．又∵FD = 2，

∴点G与点D重合，如图7．此时△EPQ与梯形ABCD

  

 的重叠部分就是梯形FPCG，其面积为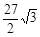

3.（3）能．4≤t≤5

解析:略