题目内容
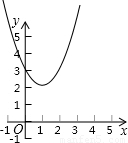
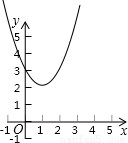
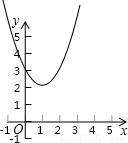
 6、若点P1(-1,y1),P2(-2,y2),P3(1,y3),都在函数y=x2-2x+3的图象上,则( )
6、若点P1(-1,y1),P2(-2,y2),P3(1,y3),都在函数y=x2-2x+3的图象上,则( )分析:抛物线y=x2-2x+3=(x-1)2+2,可知抛物线对称轴为x=1,开口向上,p1,p2在对称轴左边,y随x的增大而减小,p3为最低点故可判断y1,y2,y3的大小.
解答:解:∵y=x2-2x+3=(x-1)2+2,
∴抛物线对称轴为x=1,开口向上,
在对称轴的左边,y随x的增大而减小,
又∵1>-1>-2,
∴y2>y1>y3.故选C.
∴抛物线对称轴为x=1,开口向上,
在对称轴的左边,y随x的增大而减小,
又∵1>-1>-2,
∴y2>y1>y3.故选C.
点评:本题考查了二次函数的增减性.当二次项系数a>0时,在对称轴的左边,y随x的增大而减小,在对称轴的右边,y随x的增大而增大;a<0时,在对称轴的左边,y随x的增大而增大,在对称轴的右边,y随x的增大而减小.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
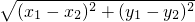 .例如:若
.例如:若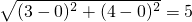 .
.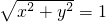 ,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.
,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.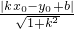 .
. 的距离.
的距离. ,其中n≠0,m>0.
,其中n≠0,m>0.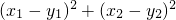 是与n无关的常数,并求出这个常数.
是与n无关的常数,并求出这个常数.