题目内容
下列说法正确的有个
(1)1的平方根是1.
(2)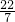 是无理数.
是无理数.
(3)顺次连接等腰梯形各边中点所得的四边形是菱形.
(4)方程x2=x的根是x=1.
(5)在一次抽奖活动中“中奖概率是 ”表示抽奖100次,就一定会中奖.
”表示抽奖100次,就一定会中奖.
(6)抛物线y= (x+2)2-3的顶点坐标是(-2,-3)
(x+2)2-3的顶点坐标是(-2,-3)
- A.2
- B.3
- C.4
- D.5
A
分析:(1)根据平方根的定义,判断即可;(2)根据无理数的定义,判断即可;(3)画出图形,连接两条对角线,根据三角形的中位线定理,即可判断;(4)方程x2=x可变为x(x-1)=0,即可得出根;(5)根据概率的定义,判断即可;(6)根据二次函数解析式及顶点坐标的表达式,即可求出;
解答: 解:(1)1的平方根是±1,故本项错误;
解:(1)1的平方根是±1,故本项错误;
(2)∵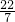 =3
=3 ,
, 是循环小数;∴
是循环小数;∴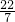 是有理数;故本项错误;
是有理数;故本项错误;
(3)如图,∵梯形ABCD是等腰梯形,
∴AC=BD,
∴EH=FG= BD,EF=HG=
BD,EF=HG= AC,
AC,
∴EH=FG=EF=HG,即四边形EFGH是菱形;故本项正确;
(4)方程x2=x,
移项得,x2-x=0,
x(x-1)=0,
∴方程的根是x=0或x=1;故本项错误;
(5)“中奖概率是 ”,概率值只是反映了事件发生的机会的大小,不是一定会发生;故本项错误;
”,概率值只是反映了事件发生的机会的大小,不是一定会发生;故本项错误;
(6)∵抛物线y= (x+2)2-3,
(x+2)2-3,
∴抛物线的顶点坐标为(-2,-3);故本项正确;
综上,说法正确的个数有2个;
故选A.
点评:本题考查了二次函数、三角形中位线及概率等知识,用到的基础知识比较多,考查了学生对知识的掌握程度.
分析:(1)根据平方根的定义,判断即可;(2)根据无理数的定义,判断即可;(3)画出图形,连接两条对角线,根据三角形的中位线定理,即可判断;(4)方程x2=x可变为x(x-1)=0,即可得出根;(5)根据概率的定义,判断即可;(6)根据二次函数解析式及顶点坐标的表达式,即可求出;
解答:
 解:(1)1的平方根是±1,故本项错误;
解:(1)1的平方根是±1,故本项错误;(2)∵
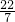 =3
=3 ,
, 是循环小数;∴
是循环小数;∴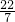 是有理数;故本项错误;
是有理数;故本项错误;(3)如图,∵梯形ABCD是等腰梯形,
∴AC=BD,
∴EH=FG=
 BD,EF=HG=
BD,EF=HG= AC,
AC,∴EH=FG=EF=HG,即四边形EFGH是菱形;故本项正确;
(4)方程x2=x,
移项得,x2-x=0,
x(x-1)=0,
∴方程的根是x=0或x=1;故本项错误;
(5)“中奖概率是
 ”,概率值只是反映了事件发生的机会的大小,不是一定会发生;故本项错误;
”,概率值只是反映了事件发生的机会的大小,不是一定会发生;故本项错误;(6)∵抛物线y=
 (x+2)2-3,
(x+2)2-3,∴抛物线的顶点坐标为(-2,-3);故本项正确;
综上,说法正确的个数有2个;
故选A.
点评:本题考查了二次函数、三角形中位线及概率等知识,用到的基础知识比较多,考查了学生对知识的掌握程度.

练习册系列答案
相关题目
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | -3 | -2 | 0 | 1 | … |
| y | … | -6 | 0 | 6 | 6 | … |
①抛物线与x轴的交点为(-2,0)(2,0); ②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是:直线
 ; ④在对称轴右侧,y随x增大而减少.
; ④在对称轴右侧,y随x增大而减少.- A.1
- B.2
- C.3
- D.4
 如图,下列说法正确的有个.
如图,下列说法正确的有个.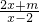 =3,下列说法正确的有个
=3,下列说法正确的有个