题目内容
(2001•天津)在Rt△ABC中,∠ACB=90°,AB=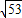 ,BC=a,AC=b.且a>b,若a,b分别是二次函数y=x2-(2k+1)x+k2-2的图象与x轴两个交点的横坐标,求a、b的值.
,BC=a,AC=b.且a>b,若a,b分别是二次函数y=x2-(2k+1)x+k2-2的图象与x轴两个交点的横坐标,求a、b的值.
【答案】分析:根据勾股定理可得出a2+b2=53,根据一元二次方程根与系数的关系可得出a+b=2k+1,ab=k2-2,联立三式即可得出k的值,进而可通过解方程求出a,b的值.
解答:解:在直角三角形ABC中,根据勾股定理有:
a2+b2=53
∵a,b分别是二次函数y=x2-(2k+1)x+k2-2的图象与x轴两个交点的横坐标
∴a+b=2k+1,ab=k2-2
∴a2+b2=(a+b)2-2ab=(2k+1)2-2k2+4=53
即k2+2k-24=0.
解得k=4,k=-6.
∵a>b>0,
∴a+b=2k+1>0
∴k>-
∴k=4
二次函数的解析式为y=x2-9x+14,
令y=0,x2-9x+14=0.
∵a>b,
∴a=7,b=2.
点评:本题主要考查了二次函数与一元二次方程的关系,一元二次方程根与系数的关系,勾股定理等知识点.
解答:解:在直角三角形ABC中,根据勾股定理有:
a2+b2=53
∵a,b分别是二次函数y=x2-(2k+1)x+k2-2的图象与x轴两个交点的横坐标
∴a+b=2k+1,ab=k2-2
∴a2+b2=(a+b)2-2ab=(2k+1)2-2k2+4=53
即k2+2k-24=0.
解得k=4,k=-6.
∵a>b>0,
∴a+b=2k+1>0
∴k>-

∴k=4
二次函数的解析式为y=x2-9x+14,
令y=0,x2-9x+14=0.
∵a>b,
∴a=7,b=2.
点评:本题主要考查了二次函数与一元二次方程的关系,一元二次方程根与系数的关系,勾股定理等知识点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
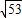 ,BC=a,AC=b.且a>b,若a,b分别是二次函数y=x2-(2k+1)x+k2-2的图象与x轴两个交点的横坐标,求a、b的值.
,BC=a,AC=b.且a>b,若a,b分别是二次函数y=x2-(2k+1)x+k2-2的图象与x轴两个交点的横坐标,求a、b的值.