题目内容
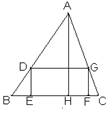
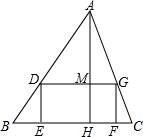如图，四边形DEFG是△ABC的内接矩形，如果△ABC的高线AH长8cm，底边BC长10cm，设DG=xcm，DE=ycm，求y关于x的函数关系式．
分析：设DE=y，则MH=y，AM=AH-MH=8-y，因为DG∥BC，可证△ADG∽△ABC，根据相似三角形对应边上高的比等于相似比，建立等式．
解答：解：设AH与DG交于点M，则AM=AH-MH=8-y，
∵DG∥BC，∴△ADG∽△ABC，
∴
=
，即
=
，
整理，得y=8-
x．
∵DG∥BC，∴△ADG∽△ABC，
∴
| AM |
| AH |
| DG |
| BC |
| 8-y |
| 8 |
| x |
| 10 |
整理，得y=8-
| 4 |
| 5 |
点评：根据条件，表示图中两相似三角形的底和高，利用相似三角形对应边上高的比等于相似比，确定函数关系式．
练习册系列答案
相关题目
如图，四边形DEFG是△ABC的内接矩形，如果△ABC的高线AH长8cm，底边BC长10cm，设DG=xcm，DE=ycm，则y关于x的函数关系式为