Question

(1)22边形的内角和是多少度？若它的每一个内角都相等，那么它的每个外角度数是多少？
(2)几边形的内角和是八边形内角和的2倍？
(3)几边形的内角和是2160°？是否存在一个多边形内角和为1000°？
(4)已知一个多边形，它的内角和等于外角和的2倍，求边数．

Answer 1

（1）22边形内角和：（22－2）×180°=3600°
因为每个内角都相等，所以每个内角为3600°÷22=（）°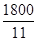
　　又因为外角与相邻内角互补，所以每个外角为180°－（）=（）°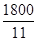
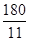另一种方法：因为多边形外角和360°，每个内角相等，那么每个外角也相等，
所以每个外角为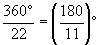
（2）设n边形的内角和是八边形内角和的2倍
　　则（n－2）×180°=2×（8－2）×180°
　　n="14"
　　∴ 14边形的内角和是八边形内角和的2倍
　　（3）设n边形的内角和是2160°
　　则（n－2）×180°=2160°
　　n=14
　　∴ 14边形的内角和是2160°
　　设n边形内角和为1000°
　　则（n－2）×180°=1000°
　　因为n不是整数，不符合题意
　　所以假设不成立
　　故不存在一个多边形内角和为1000°
　　(4)因为一个多边形内角和等于外角和的2倍
　　所以：设边数为n
　　根据题意得：（n－2）×180°=2×360°
　　n=6
　　∴ 6边形内角和等于外角和的2倍

解析