题目内容
【题目】如图,![]() 是
是![]() 的直径,延长
的直径,延长![]() 至点
至点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,切点为
,切点为![]() ,过点
,过点![]() 向
向![]() 的延长线作垂线
的延长线作垂线![]() 交该延长线于点
交该延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() .
.
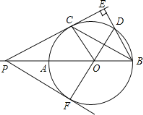
![]() 求
求![]() 的长;
的长;
![]() 连结
连结![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
①求![]() 的长;
的长;
②求证:![]() 是
是![]() 的切线.
的切线.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②见解析
;②见解析
【解析】
(1)在直角△OPC中,利用勾股定理即可得到圆的半径长,然后利用相似三角形的性质求得BE的长;
(2)①证明△OBD是等边三角形,即可求得DE的长;
②首先证明△OPC≌△OPF,根据切线的判定定理即可证得.
(1)设圆的半径是r,则OP=PA+r=1+r,OC=r,PC=![]() r.
r.
∵PC是圆的切线,∴∠PCO=90°,在直角△PCO中,PC2+OC2=OP2,即(![]() r)2+r2=(1+r)2,解得:r=1或r=﹣
r)2+r2=(1+r)2,解得:r=1或r=﹣![]() (舍去负值).
(舍去负值).
在直角△OPC中,cos∠POC=![]() =
=![]() ,∴∠POC=60°.
,∴∠POC=60°.
∵∠PCO=90°,BE⊥BC,∴BE∥OC,∴△OPC∽△BPE,∠OBD=∠POC=60°,∴![]() =
=![]() =
=![]() ,∴BE=
,∴BE=![]() OC=
OC=![]() ;
;
(2)①在△OBD中,OB=OD,∠OBD=60°,∴△OBD是等边三角形,BD=OB=1,∠BOD=60°,∴DE=BE﹣BD=![]() ﹣1=
﹣1=![]() ;
;
②∵∠POC=60°,∠BOD=60°,∴∠POF=60°,∴∠POC=∠POF.在△OPC和△OPF中,∵ ,△OPC≌△OPF(SAS),∴∠OFP=∠OCP=90°,∴PF是⊙O的切线.
,△OPC≌△OPF(SAS),∴∠OFP=∠OCP=90°,∴PF是⊙O的切线.

练习册系列答案
相关题目