题目内容
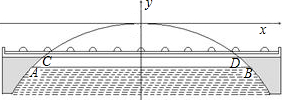
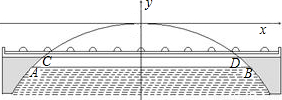
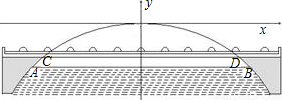
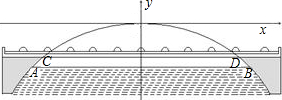
如图,有一座大桥是靠抛物线型的拱形支撑的,它的桥面处于拱形中部(如我市的中山大桥就是这种模型).已知桥面在拱形之间的宽度CD为40m,桥面CD离拱形支撑的最高点O的距离为10m,且在正常水位时水面宽度AB为48m.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)现有一辆载有救援物质的货车正以40km/h的速度必需经过此桥匀速开往乙地.当货车行驶到甲地时接到紧急通知:前方连降暴雨,造成水位以每小时0.3m的速度持续上涨(接到通知时水位已经比正常水位高出2m了,当水位到达桥面CD的高度时,禁止车辆通行).已知甲地距离此桥360km(桥长忽略不计),请问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度不得低于多少km/h?
解:(1)设所求抛物线的解析式为y=ax2,由已知点D的坐标为(20,-10)
∴400a﹦-10,
解得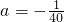 ,
,
∴所求抛物线的解析式为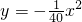 ;
;
(2)设B点坐标为(24,b),则有 ﹦14.4,
﹦14.4,
∴货车在甲地时,水面和桥面的距离为14.4-10-2﹦2.4(m),
∴水位继续上涨至桥面需要 (h),
(h),
∵40×8=320<360,
∴货车按原来速度行驶,不能安全通过此桥
又∵ ﹦45,
﹦45,
∴要使货车安全通过此桥,速度不得低于45km/h.
分析:(1)结合题意和图所示的直角坐标系,我们可以得到C(-20,-10),D(20,-10),即可求出抛物线的解析式;
(2)根据题意推出A,B两点的横坐标,代入解析式,即可得出他们的纵坐标,它们纵坐标的绝对值为水面到O点的距离为14.4,结合D点的纵坐标推出水面到桥面的距离,根据水涨的速度求出水涨到桥面的时间,然后根据时间和车到桥的距离即可求出车安全过桥的最低速度.
点评:本题考查点的坐标的求法及二次函数的实际应用.借助二次函数解决实际问题.
∴400a﹦-10,
解得
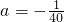 ,
,∴所求抛物线的解析式为
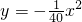 ;
;(2)设B点坐标为(24,b),则有
 ﹦14.4,
﹦14.4,∴货车在甲地时,水面和桥面的距离为14.4-10-2﹦2.4(m),
∴水位继续上涨至桥面需要
 (h),
(h),∵40×8=320<360,
∴货车按原来速度行驶,不能安全通过此桥
又∵
 ﹦45,
﹦45,∴要使货车安全通过此桥,速度不得低于45km/h.
分析:(1)结合题意和图所示的直角坐标系,我们可以得到C(-20,-10),D(20,-10),即可求出抛物线的解析式;
(2)根据题意推出A,B两点的横坐标,代入解析式,即可得出他们的纵坐标,它们纵坐标的绝对值为水面到O点的距离为14.4,结合D点的纵坐标推出水面到桥面的距离,根据水涨的速度求出水涨到桥面的时间,然后根据时间和车到桥的距离即可求出车安全过桥的最低速度.
点评:本题考查点的坐标的求法及二次函数的实际应用.借助二次函数解决实际问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目