题目内容

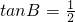如图，PC为⊙O的切线，C为切点，PAB是过O点的割线，CD⊥AB于点D，若 $数学公式$ ，PC=10cm，求△BCD的面积．

解法一：连接AC，
∵AB是⊙O的直径，点C在⊙O上，
∴∠ACB=90°
∵CD⊥AB于点D，
∴∠ADC=∠BCA=90°，
∠ACD=90°-∠BAC=∠B．
∵tanB= $\text{[math]}$ ，
∴tan∠ACD= $\text{[math]}$ ，
∴ $\text{[math]}$ ．
设AD=x（x＞0），则CD=2x，DB=4x，AB=5x．
∵PC切⊙O于点C，点B在⊙O上，
∴∠PCA=∠B，
∵∠P=∠P，
∴△PAC∽△PCB．
∴ $\text{[math]}$ ．
∵PC=10，
∴PA=5，
∵PC切⊙O于点C，PAB是⊙O的割线，
∴根据切割线定理：PC²=PA•PB，
∴10²=5（5+5x），
解得x=3，
∴AD=3，CD=6，DB=12．
∴S_△BCD= $\text{[math]}$ CD•DB= $\text{[math]}$ ×6×12=36，
即△BCD的面积为36cm²，

解法二：同解法一，由△PAC∽△PCB得 $\text{[math]}$ ，
∵PC=10，
∴PB=20，
由切割线定理，得PC²=PA•PB，
∴PA= $\text{[math]}$ ，
∴AB=PB-PA=15，
∵AD+DB=x+4x=15，
解得x=3；（x同证法一）
∴CD=2x=6，DB=4x=12，
S_△BCD= $\text{[math]}$ CD•DB= $\text{[math]}$ ×6×12=36．
即△BCD的面积为36cm²．
分析：连接AC，由弦切角定理知∠PCA=∠B，易证得△PCA∽△PBC，得PC：PB=AC：AB，而AC：AB正好是tanB，由此可求出PB的长，进而可由切割线定理求出PA的长，也就得到了AB的长；在Rt△ACB中，易证得∠ACD=∠B，那么tanB=tan∠ACD，由此可得CD=2AD，BD=2CD，即BD=4AD，联立AD+BD=AB（AB的长已求得），即可得到AD、BD、CD的长，进而可由三角形的面积公式求出△BCD的面积．
点评：此题主要考查了圆周角定理、切割线定理、弦切角定理及相似三角形的判定和性质等知识的综合应用，能够正确的构建出相似三角形，并发现PA、PB与tanB的关系是解答此题的关键．