题目内容
【题目】如图,已知△ABC中,AB=AC,BE平分∠ABC交AC于E,若∠A=90°,那么BC、BA、AE三者之间有何关系?并加以证明.
【答案】见解析
【解析】试题分析:过点E作ED⊥BC交BC于点D,可得AE=DE,再通过证Rt△BAE≌Rt△BDE推出AB=BD,再求出CD=DE=AE,则可得出答案.
解:BC、BA、AE三者之间的关系:BC=BA+AE,理由如下:
如图,过E作ED⊥BC于点D,
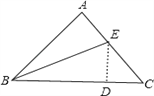
∵BE平分∠ABC,ED⊥BC,∠A=90°,
∴AE=DE,
∵在Rt△BAE和Rt△BDE中,BE=BE,AE=DE,
∴Rt△BAE≌Rt△BDE(HL),
∴BA=BD,
∵AB=AC,∠A=90°,∴∠C=45°,
∴∠CED=45°=∠C,∴DE=CD,
∴AE=CD=DE,
∴BC=BD+DC=BA+AE.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目