题目内容
已知n个数x1,x2,x3,…,xn,它们每一个数只能取0,1,-2这三个数中的一个,且
|
分析:由题可知,在x1,x2,x3,…,xn中,要想保证和为-5,平方和为19,在取值受限得情况下,可设各式中有a个1和b个-2,则可将两式变为:
,求出方程组的解.
|
解答:解:设各式中有a个1和b个-2,则可将两式变为:
,
解得
,
那么x13+x23+…+xn3=(-2)3×4+13×3=-29.
故答案为:-29.
|
解得
|
那么x13+x23+…+xn3=(-2)3×4+13×3=-29.
故答案为:-29.
点评:解此题时,关键要找准在n个数中到底有几个1、-2、0,这就需要对原题中两个式子进行分析,比较难.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
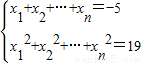 ,则x13+x23+…+xn3= .
,则x13+x23+…+xn3= .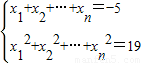 ,则x13+x23+…+xn3= .
,则x13+x23+…+xn3= .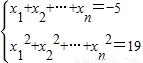 ,则x13+x23+…+xn3= .
,则x13+x23+…+xn3= .