题目内容
选择合适的方法计算：
（1））
（2）
(3)
(4)
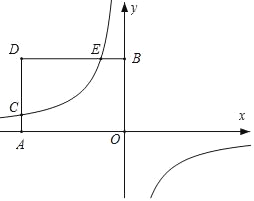
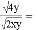如图，在平面直角坐标系中，矩形OADB的顶点A，B的坐标分别为A（﹣6，0），B（0，4）．过点C（﹣6，1）的双曲线y=（k≠0）与矩形OADB的边BD交于点E．
（1）填空：OA= ，k= ，点E的坐标为 ；
（2）当1≤t≤6时，经过点M（t﹣1，﹣t2+5t﹣）与点N（﹣t﹣3，﹣t2+3t﹣）的直线交y轴于点F，点P是过M，N两点的抛物线y=﹣x2+bx+c的顶点．
①当点P在双曲线y=上时，求证：直线MN与双曲线y=没有公共点；
②当抛物线y=﹣x2+bx+c与矩形OADB有且只有三个公共点，求t的值；
③当点F和点P随着t的变化同时向上运动时，求t的取值范围，并求在运动过程中直线MN在四边形OAEB中扫过的面积．
已知直线m∥n ， 将一块含30°角的直角三角板ABC按如图方式放置（∠ABC＝30°），其中A、B两点分别落在直线m、n上．若∠1＝20°，则∠2的度数为 （ ）
A. 20° B. 30° C. 45° D. 50°
抛物线的形状、开口方向与y＝x2﹣4x+3相同，顶点在（﹣2，1），则关系式为（ ）
A. y＝（x﹣2）2+1 B. y＝（x+2）2﹣1 C. y＝（x+2）2+1 D. y＝﹣（x+2）2+1
某创意工作室6位员工的月工资如图所示，因业务需要，现决定招聘一名新员工，若新员工的工资为4500元，则下列关于现在7位员工工资的平均数和方差的说法正确的是（ ）
A．平均数不变，方差变大 B．平均数不变，方差变小
C．平均数不变，方差不变 D．平均数变小，方差不变
有三个数，，，其中没有平方根，，则这三个数按照从小到大的顺序排列应为：________________________．
下列计算正确的是（ ）
A.
B.
C.
D.
定义新运算“?”，规定：a?b=a﹣4b，则12?（﹣1）=_____．
我国推行“一带一路”政策以来，已确定沿线有65个国家加入，共涉及总人口约达46亿人，用科学记数法表示该总人口为（ ）
A. 4.6×109 B. 46×108 C. 0.46×1010 D. 4.6×1010
（k≠0）与矩形OADB的边BD交于点E．
t2+5t﹣
）与点N（﹣t﹣3，﹣
）的直线交y轴于点F，点P是过M，N两点的抛物线y=﹣
x2﹣4x+3相同，顶点在（﹣2，1），则关系式为（ ）
（x﹣2）2+1 B. y＝
，则这三个数按照从小到大的顺序排列应为：________
a﹣4b，则12?（﹣1）=_____．