Question

【题目】如图，坐标平面上，△ABC≌△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB=BC，若A、B、C的坐标分别为（﹣3，1）、（﹣6，﹣3）、（﹣1，﹣3），D、E两点在y轴上，则F点到y轴的距离为 ．

Answer 1

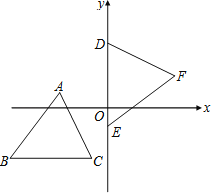
【答案】4

【解析】

试题分析：根据点A、B、C的坐标求出点A到BC的距离，再根据全等三角形对应边上的高相等求出点D到EF的距离，然后根据等腰三角形两腰上的高相等解答．

解：∵A、B、C的坐标分别为（﹣3，1）、（﹣6，﹣3）、（﹣1，﹣3），

∴点A到BC的距离为1﹣（﹣3）=4，

∵△ABC≌△DEF，

∴点D到EF的距离等于点A到BC的距离，为4，

∵AB=BC，△ABC≌△DEF，

∴DE=EF，

∴点F到DE的距离等于点D到EF的距离，为4．

故答案为4．