��Ŀ����
��ͼ�٣�����ABCD���Խ���AC��Ϊ����ֱ�������Σ�AB=3��BC=6���ֽ�Rt��ADC�Ƶ�C˳ʱ����ת90�㣬��A��ת���λ��Ϊ��E����D��ת���λ��Ϊ��F����CΪԭ�㣬��BC����ֱ��Ϊx�ᣬ�Թ���C��ֱ��BC��ֱ��Ϊy�ᣬ������ͼ�ڵ�ƽ��ֱ������ϵ��
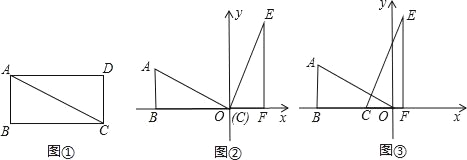
��1����ֱ��AE�Ľ���ʽ��
��2����Rt��EFC��x��ĸ�����ƽ���ƶ�����ͼ�ۣ���OC=x��0��x��9����Rt��EFC��Rt��ABO���ص��������Ϊs����x=1��x=8ʱ��s��ֵ��
��3���ڣ�2����������s�Ƿ�������ֵ�������ڣ����������ֵ����ʱx��ֵ���������ڣ���˵�����ɣ�
 ���������ν�ϵ�д�
���������ν�ϵ�д�ij��ѧ��һ�꼶��һ�о���ѧϰС��Ϊ�˽Ȿ�꼶1300��ѧ��ÿѧ�ڲμ����ʵ�����ʱ�䣬����Ը��꼶100��ѧ�������˵��飬������±���
ʱ�䣨�죩 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
�� �� | 2 | 4 | 8 | 10 | 14 | 22 | 16 | 12 | 8 | 4 |
��1�������ͳ���У��������� ������λ������ ����
��2����ȫ�����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ��
���� | Ƶ�� | Ƶ�� |
3.5��5.5 | 6 | 0.06 |
5.5��7.5 | 18 | 0.18 |
7.5��9.5 | �� �� | 0.36 |
9.5��11.5 | 28 | �� �� |
11.5��13.5 | 12 | 0.12 |
�� �� | 100 | 1.00 |
��3�������������ѧУ���꼶��ѧ���У�ÿѧ�ڲμ����ʵ���ʱ�䲻����9��Ĵ�Լ�ж����ˣ�




 C. 5 D. ��
C. 5 D. �� ��AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE=AF����AM��EF����AF=DF����DF=DN��������ȷ�Ľ����У�������
��AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE=AF����AM��EF����AF=DF����DF=DN��������ȷ�Ľ����У�������