题目内容
(2008•怀化)如图,已知正比例函数y=x与反比例函数y= 的图象交于A、B两点.
的图象交于A、B两点.(1)求出A、B两点的坐标;
(2)根据图象求使正比例函数值大于反比例函数值的x的范围.

【答案】分析:(1)A,B两点都适合这两个函数解析式,让两个函数解析式组成方程组求解即可求出两点的坐标;
(2)根据交点来分析正比例函数值大于反比例函数值的x的范围;
解答:解:(1)依题意得A、B两点的坐标满足方程组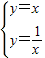
解之得, ,
,
∴A、B两点的坐标分别为:A(1,1)、B(-1,-1);
(2)根据图象知,当-1<x<0或x>1时,正比例函数值大于反比例函数值.
点评:两个函数的交点坐标即为这两个函数解析式组成的方程组的解.求自变量的取值范围都应该从交点入手思考;需注意反比例函数的自变量不能取0.
(2)根据交点来分析正比例函数值大于反比例函数值的x的范围;
解答:解:(1)依题意得A、B两点的坐标满足方程组
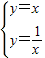
解之得,
 ,
,∴A、B两点的坐标分别为:A(1,1)、B(-1,-1);
(2)根据图象知,当-1<x<0或x>1时,正比例函数值大于反比例函数值.
点评:两个函数的交点坐标即为这两个函数解析式组成的方程组的解.求自变量的取值范围都应该从交点入手思考;需注意反比例函数的自变量不能取0.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
 S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
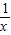 的图象交于A、B两点.
的图象交于A、B两点.
 S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.