��Ŀ����
����Ŀ����ͼ���ı���![]() �У���
�У���![]() Ϊֱ������ϵ��ԭ�㣬
Ϊֱ������ϵ��ԭ�㣬![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����
����![]() ͬʱ��ԭ��������ֱ��������˶�����
ͬʱ��ԭ��������ֱ��������˶�����![]() ��
��![]() ��ÿ��1����λ���յ�
��ÿ��1����λ���յ�![]() �˶�����
�˶�����![]() ��
��![]() ��ÿ��2����λ���յ�
��ÿ��2����λ���յ�![]() �˶���������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊ
�˶���������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊ![]() �룮
�룮

��1������![]() ��ʾ��
��ʾ��![]() ������Ϊ__________��
������Ϊ__________��
��2���Ƿ����ij��ʱ��![]() ��ʹ���Ե�
��ʹ���Ե�![]() ���ı���
���ı���![]() �е�������������Ϊ������ı���Ϊƽ���ı��Σ������ڣ������
�е�������������Ϊ������ı���Ϊƽ���ı��Σ������ڣ������![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() ��ֵΪ6��
��ֵΪ6��![]() ��
��
��������
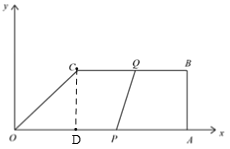
��1������A��B��C������������OA��AB��BC�ij�������C��CD��OA�����ı���CDAB�Ǿ��Σ����ù��ɶ��������OC�ij������þ���=�ٶ���ʱ�伴�ɵô𰸣�
��2����P��Q����ֱ���O��C��A��B��P��Q��C��A�������������ƽ���ı��ε����ʷֱ����tֵ������t��9����Q����λ���жϼ��ɵô𰸣�
��1����![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��
��OA=16��AB=6��BC=8��
����C��CD��OA�����ı���CDAB�Ǿ��Σ�
��CD=AB=6��OD=OA-BC=8��
��![]() ����ʱ��
����ʱ��![]() ��s����
��s����
�ߵ�Q���ٶ�Ϊÿ��2����λ��
�൱![]() ʱ��
ʱ��![]() ����ʱ��
����ʱ��![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��
���Q�ĺ�����ΪOD+CQ=2t-10+8=2t-2��������Ϊ6��
��Q������Ϊ![]() ��
��
�ʴ�Ϊ����2t-2��6��
��2���ٵ�P��Q��O��C����ƽ���ı���ʱ����OP=CQ��
�ߵ�P�ٶ�Ϊÿ��1����λ��
��OP=t��
��CQ=2t-10��
��![]() ��
��
��ã�![]() ��
��![]() ì�ܣ��ᣩ��
ì�ܣ��ᣩ��
��P��Q��A��B����ƽ���ı���ʱ����PA=QB��
��OC=10��BC=8��
��QB=18-2t��
��PA=16-t��
��![]() ��
��
��ã�![]() ����ʱ
����ʱ![]() ��
��![]() �ϣ����������⣬��ȥ
�ϣ����������⣬��ȥ
�۵�P��Q��O��B����ƽ���ı���ʱ����OP=QB��
��OP=t��QB=18-2t��
![]() ��
��
��ã�![]() ���������⣬
���������⣬
��P��Q��C��A����ƽ���ı���ʱ����PA=CQ��
��PA=16-t��CQ=2t-10��
��![]() ��
��
���![]() ���������⣬
���������⣬
����������![]() ��ֵΪ6��
��ֵΪ6��![]() ��
��









