题目内容
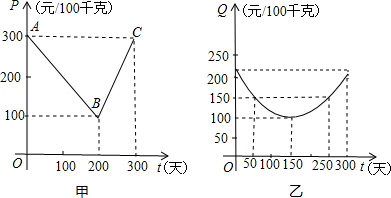
衢江区某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价 w1与上市时间t的关系用图甲的一条折线表示;西红柿的种植成本 w2与上市时间t的关系用图乙表示的抛物线段表示.
(1)求出图甲表示的市场售价 w1与时间t的函数关系式;
(2)求出图乙表示的种植成本 w2与时间t的函数关系式;
(3)市场售价减去种植成本为纯收益,当0<t≤200时,何时上市西红柿纯收益最大?(售价与成本单位:元/百千克,时间单位:天)

(1)求出图甲表示的市场售价 w1与时间t的函数关系式;
(2)求出图乙表示的种植成本 w2与时间t的函数关系式;
(3)市场售价减去种植成本为纯收益,当0<t≤200时,何时上市西红柿纯收益最大?(售价与成本单位:元/百千克,时间单位:天)
分析:(1)根据图象甲,设出函数关系式,分别找出两个点的坐标,代入即可求出w与t的函数关系式;
(2)根据图象乙,利用顶点式,即可求出函数关系式;
(3)设纯收益为h,则纯收益=市场售价-种植成本,进而利用二次函数最值求法得出即可.
(2)根据图象乙,利用顶点式,即可求出函数关系式;
(3)设纯收益为h,则纯收益=市场售价-种植成本,进而利用二次函数最值求法得出即可.
解答:解:(1)当0<t≤200,将(0,300),(200,100)代入w=at+b得
,
解得:
,
∴AB所在直线解析式为:w1=-t+300;
当200<t≤300,
将(300,300),(200,100)代入w=ct+d得
,
解得:
,
∴CB所在直线解析式为:w1=2t-300;
(2)由图象可得出二次函数顶点坐标为;(150,100),代入解析式得:
w2=k(t-150)2+100,再将(50,150)代入得出:
150=k(50-150)2+100,
解得:k=
,
∴w2=
(t-150)2+100(0<t≤300);
(3)设纯收益为y元,∵0<t≤200,则 y与 t的函数关系式:
y=-t+300-
(t-150)2-100=-
t2+
t+
,
当 t=-
=-
=50时,y有最大值.
|
解得:
|
∴AB所在直线解析式为:w1=-t+300;
当200<t≤300,
将(300,300),(200,100)代入w=ct+d得
|
解得:
|
∴CB所在直线解析式为:w1=2t-300;
(2)由图象可得出二次函数顶点坐标为;(150,100),代入解析式得:
w2=k(t-150)2+100,再将(50,150)代入得出:
150=k(50-150)2+100,
解得:k=
| 1 |
| 200 |
∴w2=
| 1 |
| 200 |
(3)设纯收益为y元,∵0<t≤200,则 y与 t的函数关系式:
y=-t+300-
| 1 |
| 200 |
| 1 |
| 200 |
| 1 |
| 2 |
| 175 |
| 2 |
当 t=-
| b |
| 2a |
| ||
2×(-
|
点评:本题考查了二次函数的应用,一次函数与分段函数,自变量取值范围在本题中都得到了体现,要根据题目给的范围,找准等量关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目