题目内容
请自取一个你喜爱的m的值,使关于x的方程x2-4x+m=0有两个不相等的非零实数根x1、x2,你取的m值为| x1 |
| x2 |
| x2 |
| x1 |
分析:因为关于x的方程x2-4x+m=0有两个不相等的非零实数根,所以△=16-4m>0.利用根与系数的关系可知x1+x2=-
=4,x1•x2=
=m,而由此可以得到
+
=
=
=
,然后代入你选择的m的值即可求出代数式值.
| b |
| a |
| c |
| a |
| x1 |
| x2 |
| x2 |
| x1 |
| ||||
| x1x2 |
| (x1+x2)2-2x1x2 |
| x1x2 |
| 16-2m |
| m |
解答:解:∵关于x的方程x2-4x+m=0有两个不相等的非零实数根,
∴△=16-4m>0,即m<4.
由根与系数的关系可知x1+x2=-
=4,x1•x2=
=m,
则
+
=
=
=
,
∴m≠0,
当m=1时,原式=14.
答案不唯一,只要m≠0时,任何值皆可.
填空答案:m=1时,原式=14.
∴△=16-4m>0,即m<4.
由根与系数的关系可知x1+x2=-
| b |
| a |
| c |
| a |
则
| x1 |
| x2 |
| x2 |
| x1 |
| ||||
| x1x2 |
| (x1+x2)2-2x1x2 |
| x1x2 |
| 16-2m |
| m |
∴m≠0,
当m=1时,原式=14.
答案不唯一,只要m≠0时,任何值皆可.
填空答案:m=1时,原式=14.
点评:本题考查了一元二次方程根的判别式和根与系数的关系.解此类题目要会用根的判别式来判断系数字母的取值范围并会把代数式变形为两根之积或两根之和的形式.一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系为:x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 .请自取一个你喜爱的m的值,使方程有两个不相等的实数根,并说明它的正确性.
.请自取一个你喜爱的m的值,使方程有两个不相等的实数根,并说明它的正确性. = .
= .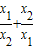 = .
= .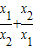 = .
= .