题目内容
如图，点A的坐标为（6，0），点B为y轴的负半轴上的一个动点，分别以OB，AB为直角边在第三、第四象限作等腰Rt△OBF，等腰Rt△ABE，连接EF交y轴于P点，当点B在y轴上移动时，PB的长度为（ ）
| A．2 | B．3 |
| C．4 | D．PB的长度随点B的运动而变化 |
解析试题分析：设B（0，m），
∵等腰Rt△OBF，∴F（m，m）.
如图，过点E作EH⊥y轴于点H，则易证Rt△ABO≌Rt△BEH，∴AO=BH，OB=HE.
∵A（6，0），B（0，m），∴E（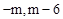
）.
设直线EF的解析式为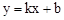
，
∴
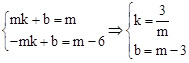.∴P
.
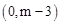∴BP=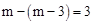
.
故选B．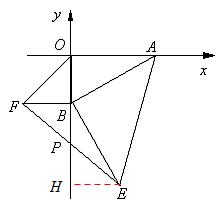
考点：1.等腰直角三角形的性质；2.全等三角形的判定和性质；3待定系数法的应用；4.直线上点的坐标与方程的关系.
练习册系列答案
相关题目
如图，过点Q（0，3.5）的一次函数与正比例函数y=2x的图象相交于点P，能表示这个一次函数图象的解析式是（ ）
A．y= | B．y= | C．y= | D．y=﹣ |
若一次函数y=ax＋b（a≠0）的图象与x轴的交点坐标为（－2，0），则抛物线y=ax2＋bx的对称轴为（ ）
| A．直线x=1 | B．直线x=－2 |
| C．直线x=－1 | D．直线x=－4 |
千米，休息了一段时间，又原路原速返回了
千米（
），再掉头沿原方向以比原速大的速度行驶，则此人离起点的距离
与时间
的函数关系的大致图象是（ ）.
，直线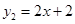
，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=1时，y1=0，y2=4，y1＜y2，此时M=0．
或
.
的图象如图所示，则反比例函数
与一次函数
在同一坐标系中的大致图象是（ ）.
已知一次函数y=kx+b的图象经过第一、二、三象限，则b的值可以是 ( )
| A．﹣2 | B．-1 | C．0 | D．2 |
一条直线y=kx+b，其中k+b=-5、kb=6，那么该直线经过（ ）
| A．第二、四象限 |
| B．第一、二、三象限 |
| C．第一、三象限 |
| D．第二、三、四象限 |
在同一坐标系中的图象可能是（ ）