题目内容
【题目】如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 .

【答案】![]() 或
或![]()
【解析】
试题分析:如图,连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P
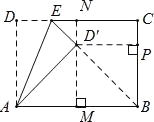
∵点D的对应点D′落在∠ABC的角平分线上,
∴MD′=PD′,
设MD′=x,则PD′=BM=x,
∴AM=AB﹣BM=7﹣x,
又折叠图形可得AD=AD′=5,
∴x2+(7﹣x)2=25,解得x=3或4,
即MD′=3或4.
在Rt△END′中,设ED′=a,
①当MD′=3时,AM=7﹣3=4,D′N=5﹣3=2,EN=4﹣a,
∴a2=22+(4﹣a)2,
解得a=![]() ,即DE=
,即DE=![]() ,
,
②当MD′=4时,AM=7﹣4=3,D′N=5﹣4=1,EN=3﹣a,
∴a2=12+(3﹣a)2,
解得a=![]() ,即DE=
,即DE=![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】去年春季,蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿,总费用是26.5万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用(万元) | 每公顷获利(万元) | |
茄子 | 1.7 | 2.4 |
西红柿 | 1.8 | 2.6 |
请解答下列问题:
(1)求出茄子和西红柿的种植面积各为多少公顷?
(2)种植场在这一季共获利多少万元?
【题目】某校对部分参加研学旅行社会实践活动的中学生的年龄(单位:岁)进行统计,结果如表:
年龄 | 12 | 12 | 14 | 15 | 16 |
人数 | 1 | 2 | 2 | 3 | 1 |
则这些学生年龄的众数和中位数分别是( )
A. 15,14B. 15,13C. 14,14D. 13,14

