题目内容
设一个三角形的三边长为正整数a,n,b,其中b≤n≤a.则对于给定的边长n,所有这样的三角形的个数是
- A.n
- B.n+1
- C.n2+n
- D.
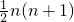
D
分析:若n=1时,三角形有一个;若n=2时,有3个;若n=3时,有6个;根据特例找出规律,即可求解.
解答:若n=1时,三角形有一个;若n=2时,有3个;若n=3时,有6个;
根据特例分析,若n=n时,有 n(n+1)个三角形.
n(n+1)个三角形.
故选D.
点评:本题考查了三角形三边关系,难度适中,关键是根据特例找出规律再进行求解.
分析:若n=1时,三角形有一个;若n=2时,有3个;若n=3时,有6个;根据特例找出规律,即可求解.
解答:若n=1时,三角形有一个;若n=2时,有3个;若n=3时,有6个;
根据特例分析,若n=n时,有
 n(n+1)个三角形.
n(n+1)个三角形.故选D.
点评:本题考查了三角形三边关系,难度适中,关键是根据特例找出规律再进行求解.

练习册系列答案
相关题目
设一个三角形的三边长分别是3,1-2m,8,则m的取值范围是( )
A、0<m<
| ||
| B、-5<m<-2 | ||
| C、-2<m<5 | ||
D、
|
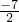 <m<-1
<m<-1
 <m<-1
<m<-1
 <m<-1
<m<-1