题目内容
 (2012•菏泽)牡丹花会前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
(2012•菏泽)牡丹花会前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)菏泽市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
分析:(1)利用表中x、y的各组对应值作为点的坐标,在坐标系中描出即可,再根据点的分布得出y与x的函数关系式,求出即可;
(2)根据利润=销售总价-成本总价,由(1)中函数关系式得出W=(x-10)(-10x+700),进而利用二次函数最值求法得出即可;
(3)利用二次函数的增减性,结合对称轴即可得出答案.
(2)根据利润=销售总价-成本总价,由(1)中函数关系式得出W=(x-10)(-10x+700),进而利用二次函数最值求法得出即可;
(3)利用二次函数的增减性,结合对称轴即可得出答案.
解答: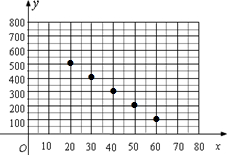 解:(1)画图如图:
解:(1)画图如图:
由图可猜想y与x是一次函数关系,
设这个一次函数为y=kx+b(k≠0),
∵这个一次函数的图象经过(20,500)、(30,400)这两点,
∴
,
解得:
,
∴函数关系式是y=-10x+700.
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得:
W=(x-10)(-10x+700),
=-10x2+800x-7000,
=-10(x-40)2+9000,
∴当x=40时,W有最大值9000元.
(3)对于函数W=-10(x-40)2+9000,
当x≤35时,W的值随着x值的增大而增大,
故销售单价定为35元∕件时,工艺厂试销该工艺品每天获得的利润最大.
 解:(1)画图如图:
解:(1)画图如图:由图可猜想y与x是一次函数关系,
设这个一次函数为y=kx+b(k≠0),
∵这个一次函数的图象经过(20,500)、(30,400)这两点,
∴
|
解得:
|
∴函数关系式是y=-10x+700.
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得:
W=(x-10)(-10x+700),
=-10x2+800x-7000,
=-10(x-40)2+9000,
∴当x=40时,W有最大值9000元.
(3)对于函数W=-10(x-40)2+9000,
当x≤35时,W的值随着x值的增大而增大,
故销售单价定为35元∕件时,工艺厂试销该工艺品每天获得的利润最大.
点评:此题主要考查了二次函数的应用以及待定系数法求一次函数解析式以及二次函数增减性应用等知识,此题难度不大是中考中考查重点内容.

练习册系列答案
相关题目
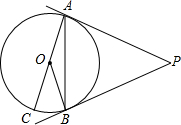 (2012•菏泽)如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC=
(2012•菏泽)如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC=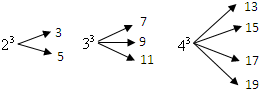 (2012•菏泽)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,
(2012•菏泽)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,