题目内容
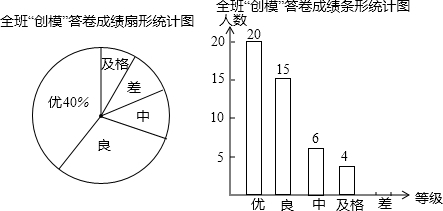
“创建环保模范城,共享绿色沙坪坝”,沙坪坝区政府决定在南开中学某年级中随机抽取某个班就“创模”知识的了解情况进行问卷调查,然后将该班答卷成绩按“优”、“良”、“中”、“及格”、“差”五个等级进行分析,并绘制了两幅不完整的扇形统计图和条形统计图.
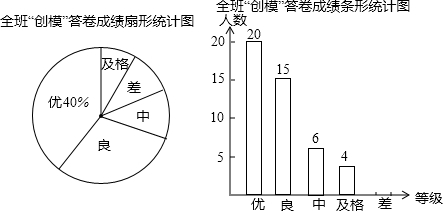
(1)该班共有______人,其中成绩得“差”的人数占______%.并补全条形统计图;
(2)为了让更多的人了解和参与到“创模”活动中去,学校决定从成绩得“差”的所有同学中选派2名,参加沙区政府组织的“创模知识讲座”,其中成绩得“差”的同学中有小明和小丽.请用列表或画树状图的方法,求出所选两位同学恰好是小明和小丽参加此讲座的概率.
解:(1)20÷40%=50人,
得“差”的人数为:50-20-15-6-4=5人
得“差”的人数的百分比为:5÷50=10%.
故答案为:50,10,
补全图形为:

(2)设5个得“差”的学生分别是:甲、乙,丙,小明、小丽.由题意列表为:
共有20种情况,其中是小明、小丽的有2种.
故P(小明、小丽)=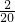 =
= .
.
分析:(1)用优的频数÷频率就可以求出全班总人数.用总人数减去优、良、中、及格的人数就是差的人数,就可以补全条形统计图.再用差的人数÷总人数就可以求出得“差”的人数的百分数.
(2)由(1)的结论,用列表法求出求出总共的情况,从而可以求出是小明和小丽的概率.
点评:本题考查了条形统计图的运用,扇形统计图的运用及运用列表法求概率的运用.在解答时要善于运用图表提供的信息求出相应的数据是解答的关键.
得“差”的人数为:50-20-15-6-4=5人
得“差”的人数的百分比为:5÷50=10%.
故答案为:50,10,
补全图形为:

(2)设5个得“差”的学生分别是:甲、乙,丙,小明、小丽.由题意列表为:
| 甲 | 乙 | 丙 | 小明 | 小丽 | |
| 甲 | (甲、乙) | (甲、丙) | (甲、小明) | (甲、小丽) | |
| 乙 | (乙、甲) | (乙、丙) | (乙、小明) | (乙、小丽) | |
| 丙 | (丙、甲) | (丙、乙) | (丙、小明) | (丙、小丽) | |
| 小明 | (小明、甲) | (小明、乙) | (小明、丙) | (小明、小丽) | |
| 小丽 | (小丽、甲) | (小丽、乙) | (小丽、丙) | (小丽、小明) |
故P(小明、小丽)=
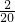 =
= .
.分析:(1)用优的频数÷频率就可以求出全班总人数.用总人数减去优、良、中、及格的人数就是差的人数,就可以补全条形统计图.再用差的人数÷总人数就可以求出得“差”的人数的百分数.
(2)由(1)的结论,用列表法求出求出总共的情况,从而可以求出是小明和小丽的概率.
点评:本题考查了条形统计图的运用,扇形统计图的运用及运用列表法求概率的运用.在解答时要善于运用图表提供的信息求出相应的数据是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目