题目内容
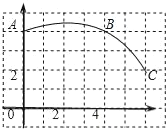
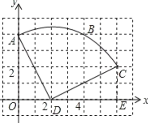
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ;扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
【答案】(1)(2,0);(2)2![]() ,90;(3)
,90;(3)![]()
【解析】
(1)作AB、BC的垂直平分线,两垂直平分线的交代即为点D,再根据坐标轴上点的坐标特征可得到点D的坐标;
(2)连接DA、DC,利用勾股定理求出AD的长,即⊙D的半径;再利用SAS证得△AOD≌△DEC,根据全等三角形的性质可得∠OAD=∠CDE,然后求出∠ADC的度数即可;
(3)设出圆锥的底面半径,再根据圆锥的底面周长等于侧面展开图即扇形的弧长,即可求出该圆锥的底面半径.
(1)如图,分别作AB、BC的垂直平分线,两线交于点D,
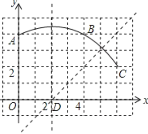
∴D点的坐标为(2,0).
(2)连接DA、DC,如图,
则AD=![]() ,
,
即⊙D的半径为![]() .
.
∵OD=CE,OA=DE=4,
∠AOD=∠CEO=90°,
∴△AOD≌△DEC,
∴∠OAD=∠CDE,
∴∠ADO+∠CDE=∠ADO+∠OAD=90°,
∴∠ADC=90°,
即扇形DAC的圆心角度数为90°.
(3)设圆锥的底面半径是r,
则![]() ,
,
∴![]() ,
,
即该圆锥的底面半径为![]() .
.

练习册系列答案
相关题目