题目内容
 (2013•东城区二模)如图,在平面直角坐标系中,已知⊙O的半径为1,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
(2013•东城区二模)如图,在平面直角坐标系中,已知⊙O的半径为1,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )分析:设直线AB的解析式为y=x+b,当直线与圆相切时切点为C,连接OC,则OC=1,由于直线AB与x轴正方向夹角为45°,所以△AOC是等腰直角三角形,故OC=PC=1再根据勾股定理求出OA的长即可.
解答: 解:∵直线AB与x轴正方向夹角为45°,
解:∵直线AB与x轴正方向夹角为45°,
∴设直线AB的解析式为y=x+b,切点为C,连接OC,
∵⊙O的半径为1,
∴△AOC是等腰直角三角形,
∴OC=PC=1,
∴OA=
=
,
∴P(
,0),
同理可得,当直线与x轴负半轴相交时,P(-
,0),
∴-
≤x≤
.
故选D.
 解:∵直线AB与x轴正方向夹角为45°,
解:∵直线AB与x轴正方向夹角为45°,∴设直线AB的解析式为y=x+b,切点为C,连接OC,
∵⊙O的半径为1,
∴△AOC是等腰直角三角形,
∴OC=PC=1,
∴OA=
| 12+12 |
| 2 |
∴P(
| 2 |
同理可得,当直线与x轴负半轴相交时,P(-
| 2 |
∴-
| 2 |
| 2 |
故选D.
点评:本题考查的是直线与圆的位置关系,熟知直线和圆的三种位置关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
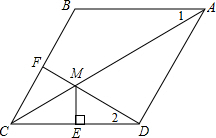 (2013•东城区二模)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E.
(2013•东城区二模)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E.