题目内容
问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.
小明的做法及思路
小明添加了条件:∠DAB=∠BCD.他的思路是:分两种情况画图①、图②,在两幅图中,
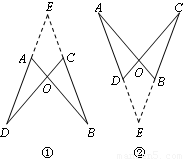
都作直线DA、BC,两直线交于点E.
由∠DAB=∠BCD,可得∠EAB=∠ECD.
∵AB=CD,∠E=∠E,
∴△EAB≌△ECD.∴EB=ED,EA=EC.
图①中ED-EA=EB-EC,即AD=CB.
图②中EA-ED=EC-EB,即AD=CB.
又∵∠DAB=∠BCD,∠AOD=∠COB,
∴△AOD≌△COB.
数学老师的观点:
(1)数学老师说:小明添加的条件是错误的,请你给出解释.
你的想法:
(2)请你重新添加一个满足问题要求的条件
,并说明理由.
【答案】
(1)可画出下面的反例:图中,AB=CD,DA∥BC.此时,虽有∠A=∠C,但△AOD与△COB不全等;(2)答案不唯一,如OA=OC.
【解析】
试题分析:根据全等三角形的判定结合图形的特征求解即可.
(1)可画出下面的反例:
图中,AB=CD,DA∥BC.
此时,虽有∠A=∠C,但△AOD与△COB不全等;
(2)答案不唯一,如OA=OC.
理由如下:
∵AB=CD,OA=OC,
∴AB-OA=CD-OC,即OB=OD.
∵∠AOD=∠COB,
∴△AOD≌△COB.
考点:全等三角形的判定和性质
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.
问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB. 小明的做法及思路
小明的做法及思路 分两种情况画图①、图②,在两幅图中,
分两种情况画图①、图②,在两幅图中,