Question

阅读下面的题目及分析过程，再回答问题．
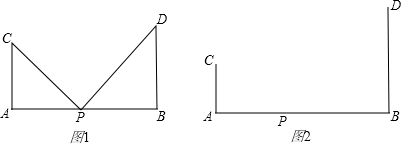
设x，y为正实数，且x+y=6，求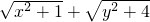的最小值．分析：（1）如图（1），作长为6的线段AB，过A、B两点在同侧各做AC⊥AB，BD⊥AB，使AC=1，BD=2．
（2）设P是AB上的一个动点．设PA=x，PB=y，则x+y=6，连接PC、PD，则PC=，PD=
（3）只要在AB上找到使PC+PD为最小的点P的位置，就可以计算出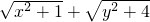的最小值．问题：①在图（2）中作出符合上述要求的点．
②求AP的长？
③通过上述作图，计算当x+y=6时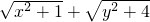，的最小值为________．
解决问题：
为了丰富学生的课余生活，石家庄外国语学校决定举办一次机器人投篮大赛．规则是：操纵者站在距线段AB 2米的C处，如图（3）使机器人从A点出发，到C处取到篮球，然后行驶到B处，将篮球投入设在B处的篮筐内，用时少的即为胜利者，为了获得胜利，请你画出C的最佳位置；并求当AB=3米时机器人行驶的最短路程？

Answer 1

解：①延长线段CA，在延长线上截取AC′=AC，连接C′D于AB的交点即为点P，
此时CP+PD最短，∴点P为所求作的点；

②∵AC=AC′，∠CAP=∠C′AP=90°，AP=AP，
∴△CAP≌△C′AP，
∵∠APC′=∠APC，又∠APC′=∠DPB，
∴∠APC=∠DPB，又∠CAP=∠B=90°，
∴△APC∽△BPD，
∴=，即=，
解得：AP=2；

③根据题意可知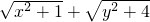：的最小值为线段C′D的长，
延长DB，过C′作C′E⊥BD，垂足为点E，
则AC=AC′=BE=1，故DE=3，又C′E=x+y=6，
在直角三角形DC′E中，根据勾股定理得：C′D=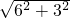=3，
∴当x+y=6时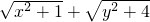，的最小值为3；
解决问题：
根据题意，画图形如下：
过点A作直线l的垂线，以垂足为圆心，在直线l的上方找出点A关于l的对称点A′，
连接A′B与直线l交于点C，此时AC=AC′，故AC+CB最短，∴点C为所求作的点，
由对称可知AA′=4，又AB=3，
在直角三角形A′AB中，根据勾股定理得：AC+CB=A′C+CB=A′B==5米，
则机器人行驶的最短距离为5米．
故答案为：3．
分析：①找出点C关于AB的对称点C′，连接C′D于AB交于点P，即为PC+PD为最小时所求的点的位置；
②根据对称，利用“SAS”证明△CAP≌△C′AP，得到∠APC′=∠APC，再根据对顶角相等和等量代换得到∠APC=∠CPB，又根据∠CAP=∠B=90°，由两对对应角相等的两三角形相似得到△APC∽△BPC，根据相似三角形的对应边成比例即可求出AP的长；
③根据题中的分析和作图可知：当x+y=6时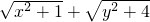，的最小值为线段C′D的长，所以延长DB，过C′作C′E⊥DE，得到△DC′E为直角三角形，由CC′和C′E，根据勾股定理即可求出C′D的长；
解决问题：
作出点A关于l的对称点A′，连接A′B交l于点C，故点C为所求的最佳位置，由作图可知AA′的长，又AB的长，根据勾股定理即可求出A′B的长，求出AC+CB的最短距离，即为机器人走的最短距离．
点评：此题综合考查了对称知识，三角形相似的判断与性质，直角三角形的性质以及作图的方法．作图时得到的最短距离的原因是两点之间线段最短．