题目内容
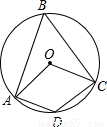
（2003•无锡）如图，四边形ABCD内接于⊙O，∠AOC=100°，则∠B= 度，∠D= 度．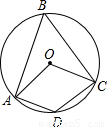
【答案】分析：已知了圆心角∠AOC的度数，欲求∠B的度数，可利用圆周角和圆心角的关系求解；进而可根据圆内接四边形的对角互补，求得∠D的度数．
解答：解：由圆周角定理得：∠B=
∠AOB=
×100=50°；
∵四边形ABCD内接于⊙O，
∴∠B+∠D=180°；
∴∠D=180°-∠B=180°-50°=130°．
点评：本题考查的是圆周角定理及圆内接四边形的性质．
解答：解：由圆周角定理得：∠B=
∠AOB=×100=50°；∵四边形ABCD内接于⊙O，
∴∠B+∠D=180°；
∴∠D=180°-∠B=180°-50°=130°．
点评：本题考查的是圆周角定理及圆内接四边形的性质．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
