Question

设x是实数，y=|x-1|+|x+1|．下列四个结论：
Ⅰ．y没有最小值；
Ⅱ．只有一个x使y取到最小值；
Ⅲ．有有限多个x（不止一个）使y取到最大值；
Ⅳ．有无穷多个x使y取到最小值．
其中正确的是（　　）

A、Ⅰ

B、Ⅱ

C、Ⅲ

D、Ⅳ

Answer 1

分析：|x|的几何意义是表示数轴上点x到原点的距离．类似地可知，|x-a|的几何意义是表示数轴上点x到点a的距离．所以原问题可转化为求x取哪些值时，数轴上点x到点1与点-1的距离之和为最小．

解答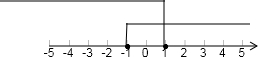：解：从数轴上可知，区间[-1，1]上的任一点x到点1与点-1的距离之和均为2；区间[-1，1]之外的点x 到点1与点-1的距离之和均大于2．
所以函数y=|x-1|+|x+1|当-1≤x≤1时，取得最小值2．
Ⅰ、y在区间[-1，1]上取得最小值2；故本选项错误；
Ⅱ、y在区间[-1，1]上的任一点x到点1与点-1的距离之和均为2；故本选项错误；
Ⅲ、y在区间[-1，1]之外的点x 到点1与点-1的距离之和均大于2，且无限大，所以y在区间[-1，1]之外的点没有最大值；故本选项错误；
Ⅳ、y在区间[-1，1]上的任一点x到点1与点-1的距离之和均为最小值2，所以有无穷多个x使y取到最小值．故本选项正确；
故选D．

点评：本题考查了函数最值问题．解题时，利用了绝对值的几何意义，借助数形结合，常常会得到妙解．