��Ŀ����
��ͼ1����֪������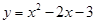 ��x�ύ�ڵ�A�͵�B����y���ཻ�ڵ�C��
��x�ύ�ڵ�A�͵�B����y���ཻ�ڵ�C��
1.��A��B��C���������
2.��DΪ����CB�ϵ�һ���㣨��D��B���غϣ�������B��x��Ĵ���BE���Ե�DΪ�����������y��(x��t)2��h�ཻ�ڵ�E���ӡ�ADE�͡�ADB����ѡһ�������Σ��������������ڡ�ABE�����ʱ��t��ֵ����������ʾ��1��ֻѡȡһ����������⼴�ɣ�2���������������ζ����˽��ֻ����һ�������֣���
3.��ͼ2������P��ֱ��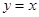 �ϵ�һ�����㣬��Q���������ϵ�һ�����㣬���Ե�O��C��P��QΪ������ı���Ϊֱ�����Σ�����Ӧ�ĵ�P�����꣮
�ϵ�һ�����㣬��Q���������ϵ�һ�����㣬���Ե�O��C��P��QΪ������ı���Ϊֱ�����Σ�����Ӧ�ĵ�P�����꣮
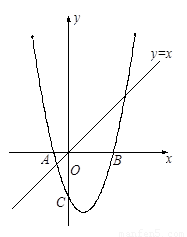
���𰸡�
1.A����1��0����B��3��0��,C��0����3��
2.��ѡȡ��ADE��t1����t2�� ��ѡȡ��ADB��t��1
3.��-3��-3������-1��-1������2��2������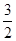 ��
��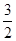 ������-
������-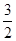 ��-
��-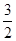 ����
����
������������������������������ף�����ע�⣨2����Щ�Ѷȣ�ֱ�ߺ����������ϡ�

��ϰ��ϵ�д�
�����Ŀ

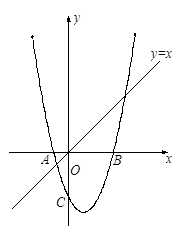
 ��x �ύ������A��B���䶥��ΪC��
��x �ύ������A��B���䶥��ΪC��
 ƽ���ı��Σ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
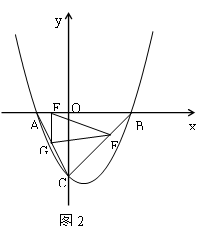
ƽ���ı��Σ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�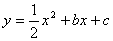 ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����OB =" 2OA" = 4��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����OB =" 2OA" = 4��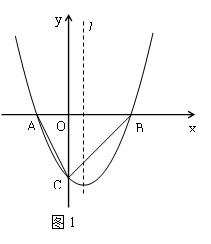
 ����λ���ȵ��ٶ����յ�C�˶�������E��EG//y�ᣬ��AC�ڵ�G����ͼ2������E��F����ͬʱ�������˶�ʱ��Ϊt����tΪ��ֵʱ����EFG������ǡ�ABC�������
����λ���ȵ��ٶ����յ�C�˶�������E��EG//y�ᣬ��AC�ڵ�G����ͼ2������E��F����ͬʱ�������˶�ʱ��Ϊt����tΪ��ֵʱ����EFG������ǡ�ABC�������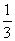 ��
��