题目内容
如图,已知在Rt△ABC中,∠C=Rt∠,a、b、c分别是∠A,∠B,∠C的对边,且a:b=3:4,a+b=c+4.(1)求a、b长;
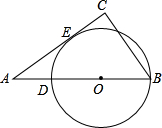
(2)若D是AB上的定点,以BD为直径的⊙O恰好切AC于点E,求⊙O的半径r;
(3)若⊙O的圆心O是AB上的动点,求⊙O的半径r在怎样的取值范围内,能使⊙O与AC相切,
 且与BC所在直线相交?
且与BC所在直线相交?
分析:(1)根据a:b=3:4,设a=3k,b=4k.根据勾股定理,得c=5k;再根据a+b=c+4,求得k的值,从而求得a,b的长;
(2)连接OE,得到OE⊥AC.根据OE∥BC,得到相似三角形,根据相似三角形的对应边的比相等,即可求解;
(3)此题首先可以求得圆和AC,BC相切时,确定r的最小值,再进一步根据BC的长确定r的最大值.
(2)连接OE,得到OE⊥AC.根据OE∥BC,得到相似三角形,根据相似三角形的对应边的比相等,即可求解;
(3)此题首先可以求得圆和AC,BC相切时,确定r的最小值,再进一步根据BC的长确定r的最大值.
解答:解:(1)设a=3k,b=4k.
根据勾股定理,得c=5k.
又a+b=c+4,
3k+4k=5k+4,
k=2.
则a=6,b=8.
(2)连接OE,得到OE⊥AC.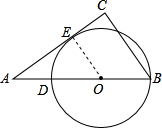
则OE∥BC.
∴
=
,即
=
,r=
.
(3)设⊙O和AC,BC相切于点M,N.
连接OM,ON.
设此时圆的半径是r,OB=x.
∵OM∥BC,
∴
=
.
即
=
.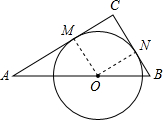
∵ON∥AC,
∴
=
.
即
=
,
解得r=
.
又BC=6,
所以
<r≤6.
根据勾股定理,得c=5k.
又a+b=c+4,
3k+4k=5k+4,
k=2.
则a=6,b=8.
(2)连接OE,得到OE⊥AC.

则OE∥BC.
∴
| OE |
| BC |
| OA |
| AB |
| r |
| 6 |
| 10-r |
| 10 |
| 15 |
| 4 |
(3)设⊙O和AC,BC相切于点M,N.
连接OM,ON.
设此时圆的半径是r,OB=x.
∵OM∥BC,
∴
| OM |
| BC |
| OA |
| AB |
即
| r |
| 6 |
| 10-x |
| 10 |

∵ON∥AC,
∴
| ON |
| AC |
| OB |
| AB |
即
| r |
| 8 |
| x |
| 10 |
解得r=
| 24 |
| 7 |
又BC=6,
所以
| 24 |
| 7 |
点评:此题综合运用了切线的性质和相似三角形的判定和性质.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 (2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( )
(2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( ) 如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.
如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长. 如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC=
如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC= 如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图:
如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图: