题目内容
B船在A船的西偏北45°处,两船相距10| 2 |
分析:作出A船、B船的行进路线图形,找到B船的速度为A船速度的2倍的等量关系,设AE=x,于是BD=2x,并且在直角△CDE中,DE为斜边,根据CD,CE计算DE,
解答: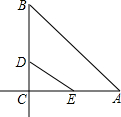 解:如图,
解:如图,
设经过t小时后,A船、B船分别航行到E,D,设AE=x,于是BD=2x.
由AB=10
,得AC=BC=10km.
∴EC=|10-x|,DC=|10-2x|.
∴DE=
=
km.
当x=6时,DE=2
km最小.
故答案为:2
.
 解:如图,
解:如图,设经过t小时后,A船、B船分别航行到E,D,设AE=x,于是BD=2x.
由AB=10
| 2 |
∴EC=|10-x|,DC=|10-2x|.
∴DE=
| (10-x)2+(10-2x)2 |
=
| 5(x-6)2+20 |
当x=6时,DE=2
| 5 |
故答案为:2
| 5 |
点评:本题考查了勾股定理在实际生活中的应用,考查了最小值问题,本题中找到B船的速度是A船的速度的2倍,并且在直角△CDE中求x是解题的关键.

练习册系列答案
相关题目
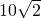 km,若A船向西航行,B船同时向南航行,且B船的速度为A船速度的2倍,那么A、B两船的最近距离是________km.
km,若A船向西航行,B船同时向南航行,且B船的速度为A船速度的2倍,那么A、B两船的最近距离是________km.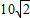 km,若A船向西航行,B船同时向南航行,且B船的速度为A船速度的2倍,那么A、B两船的最近距离是 km.
km,若A船向西航行,B船同时向南航行,且B船的速度为A船速度的2倍,那么A、B两船的最近距离是 km.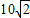 km,若A船向西航行,B船同时向南航行,且B船的速度为A船速度的2倍,那么A、B两船的最近距离是 km.
km,若A船向西航行,B船同时向南航行,且B船的速度为A船速度的2倍,那么A、B两船的最近距离是 km.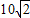 km,若A船向西航行,B船同时向南航行,且B船的速度为A船速度的2倍,那么A、B两船的最近距离是 km.
km,若A船向西航行,B船同时向南航行,且B船的速度为A船速度的2倍,那么A、B两船的最近距离是 km.