题目内容
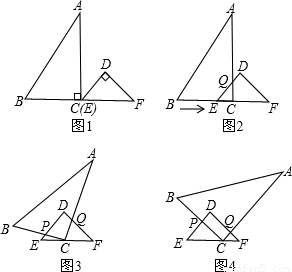
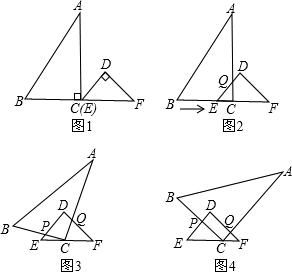
 已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
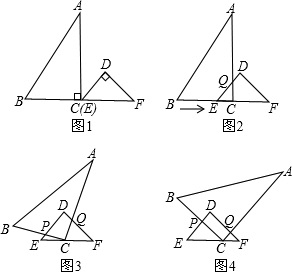
已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.运动一:如图2,△ABC从图1的位置出发,以1cm/s的速度沿EF方向向右匀速运动,DE与AC相交于点Q,当点Q与点D重合时暂停运动;
运动二:在运动一的基础上,如图3,RT△ABC绕着点C顺时针旋转,CA与DF交于点Q,CB与DE交于点P,此时点Q在DF上匀速运动,速度为
| 2 |
运动三:在运动二的基础上,如图4,RT△ABC以1cm/s的速度沿EF向终点F匀速运动,直到点C与点F重合时为止.
设运动时间为t(s),中间的暂停不计时,
解答下列问题
(1)在RT△ABC从运动一到最后运动三结束时,整个过程共耗时
(2)在整个运动过程中,设RT△ABC与RT△DEF的重叠部分的面积为S(cm2),求S与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)在整个运动过程中,是否存在某一时刻,点Q正好在线段AB的中垂线上,若存在,求出此时t的值;若不存在,请说明理由.
分析:(1)运动一,停止时,EC=4cm,用时为:4÷1=4秒;运动二,停止时,DQ=2
cm,用时为:2
÷
=2秒;运动三,点C与点F重合时,CF=4cm,用时为:4÷1=4秒;综上,总用时为:4+2+4=10(秒);
(2)运动一,Rt△ABC与Rt△DEF的重叠部分为直角△QCE的面积,表示出即可;运动二,连接CD,可得∠E=∠CDQ,∠ECP=∠ECQ,EC=DC,所以△ECP≌△DCQ,RT△ABC与RT△DEF的重叠部分不变:y=8(4<t<6);运动三,四边形QDPC为矩形,CF=4-(t-6)=10-t,EC=8-CF=t-2,所以,S矩形QDPC=
(t-2)×
(10-t)=-
t2+6t-10;
(3)点Q在线段AB的中垂线上,连接BQ,可得AQ=QB,所以,AC-CQ=
,又AC=16cm,BC=12cm,得,CQ=3.5cm,又由∠DEF=45°,所以,EC=3.5cm,解答出即可.
| 2 |
| 2 |
| 2 |
(2)运动一,Rt△ABC与Rt△DEF的重叠部分为直角△QCE的面积,表示出即可;运动二,连接CD,可得∠E=∠CDQ,∠ECP=∠ECQ,EC=DC,所以△ECP≌△DCQ,RT△ABC与RT△DEF的重叠部分不变:y=8(4<t<6);运动三,四边形QDPC为矩形,CF=4-(t-6)=10-t,EC=8-CF=t-2,所以,S矩形QDPC=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(3)点Q在线段AB的中垂线上,连接BQ,可得AQ=QB,所以,AC-CQ=
| BC2+CQ2 |
解答:解:(1)根据题意得,
运动一:
∵△DEF是等腰三角形,∠ACB=90°,EF=8cm,
∴EC=4cm,
∴运动一所用时间为:4÷1=4(秒),
运动二:
∵当QC⊥DF时暂停旋转,
∵CD=CF,
∴DQ=QF=2
cm
∴运动二所用时间为:2
÷
=2(秒),
运动三:
∵CF=4cm,
∴运动三所用的时间为:4÷1=4(秒),
∴整个过程共耗时4+2+4=10(秒);
故答案为:10;
(2)运动一:如图2,
设EC为tcm,则CQ为tcm,
∴S△ECQ=
×t×t,
∴S与t之间的函数关系式为:y=
t2(0≤t≤4),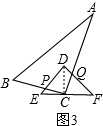
运动二:如图3,
连接CD,在△ECP和△DCQ中,
∵
∴△ECP≌△DCQ(ASA),
∴S与t之间的函数关系式为:y=8(4<t<6),
运动三:如图4,
四边形QDPC为矩形,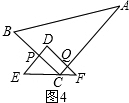
∴CF=4-(t-6)=10-t,
EC=8-CF=t-2,
∴S矩形QDPC=
(t-2)×
(10-t),
=-
t2+6t-10;
S与t之间的函数关系式为:y=-
t2+6t-10(6≤t≤10);
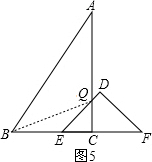 (3)存在点Q,理由如下:
(3)存在点Q,理由如下:
如图5,运动一:
∵点Q在线段AB的中垂线上,连接BQ,
∴AQ=QB,
∴AC-CQ=
,
又∵AC=16cm,BC=12cm,
解得,CQ=3.5cm,
∵∠DEF=45°,
∴EC=3.5cm,
此时,t为:3.5÷1=3.5秒.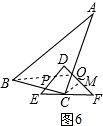
如图6,运动二:
同理:CQ=3.5,
过点C作CM⊥DF交DF于点M,CM=2
,
在Rt△QCM中,QM=
=
,
∴DQ=2
-
,
∴t=(2
-
)÷
+4=6-
;
运动三时,CQ最大为2
<3.5,
所以无解.
综上,t=3.5或6-
时,点Q正好在线段AB的中垂线上.
运动一:
∵△DEF是等腰三角形,∠ACB=90°,EF=8cm,
∴EC=4cm,
∴运动一所用时间为:4÷1=4(秒),
运动二:
∵当QC⊥DF时暂停旋转,
∵CD=CF,
∴DQ=QF=2
| 2 |
∴运动二所用时间为:2
| 2 |
| 2 |
运动三:
∵CF=4cm,
∴运动三所用的时间为:4÷1=4(秒),
∴整个过程共耗时4+2+4=10(秒);
故答案为:10;
(2)运动一:如图2,
设EC为tcm,则CQ为tcm,
∴S△ECQ=
| 1 |
| 2 |
∴S与t之间的函数关系式为:y=
| 1 |
| 2 |

运动二:如图3,
连接CD,在△ECP和△DCQ中,
∵
|
∴△ECP≌△DCQ(ASA),
∴S与t之间的函数关系式为:y=8(4<t<6),
运动三:如图4,
四边形QDPC为矩形,

∴CF=4-(t-6)=10-t,
EC=8-CF=t-2,
∴S矩形QDPC=
| ||
| 2 |
| ||
| 2 |
=-
| 1 |
| 2 |
S与t之间的函数关系式为:y=-
| 1 |
| 2 |
 (3)存在点Q,理由如下:
(3)存在点Q,理由如下:如图5,运动一:
∵点Q在线段AB的中垂线上,连接BQ,
∴AQ=QB,
∴AC-CQ=
| BC2+CQ2 |
又∵AC=16cm,BC=12cm,
解得,CQ=3.5cm,
∵∠DEF=45°,
∴EC=3.5cm,
此时,t为:3.5÷1=3.5秒.

如图6,运动二:
同理:CQ=3.5,
过点C作CM⊥DF交DF于点M,CM=2
| 2 |
在Rt△QCM中,QM=
| CQ2-CM2 |
| ||
| 2 |
∴DQ=2
| 2 |
| ||
| 2 |
∴t=(2
| 2 |
| ||
| 2 |
| 2 |
| ||
| 4 |
运动三时,CQ最大为2
| 2 |
所以无解.
综上,t=3.5或6-
| ||
| 4 |
点评:本题考查了全等三角形的判定与性质、线段的垂直平分线、旋转、平移的性质等,要注意的是(2)中,要根据P点的不同位置进行分类求解;(3)中要确定点Q的位置,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.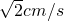 ,当QC⊥DF时暂停旋转;
,当QC⊥DF时暂停旋转; ,当QC⊥DF时暂停旋转;
,当QC⊥DF时暂停旋转;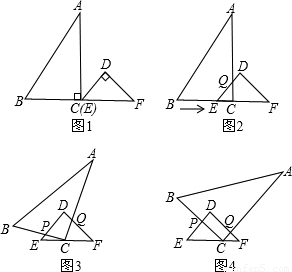
 ,当QC⊥DF时暂停旋转;
,当QC⊥DF时暂停旋转;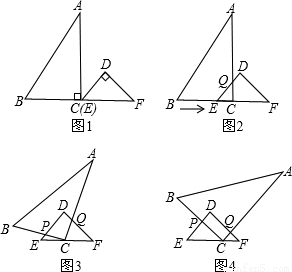
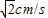 ,当QC⊥DF时暂停旋转;
,当QC⊥DF时暂停旋转;