题目内容
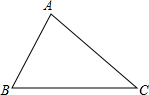 第十届亚运会在广东召开,有三名运动员分别下榻在A、B、C三个宾馆,三个宾馆由三条道路相连,如图所示.(1)为建一个公共活动场地P到三条道路的距离相等.请用尺方法作出点P,使得点P落在△ABC内部.保留作图痕迹.不要求写作法.(2)如果∠ACB=α°,那么∠APB=
第十届亚运会在广东召开,有三名运动员分别下榻在A、B、C三个宾馆,三个宾馆由三条道路相连,如图所示.(1)为建一个公共活动场地P到三条道路的距离相等.请用尺方法作出点P,使得点P落在△ABC内部.保留作图痕迹.不要求写作法.(2)如果∠ACB=α°,那么∠APB=分析:(1)作△ABC两内角的角平分线,交点就是P;
(2)根据三角形内角和定理可得∠APB=180°-(∠BAP+∠ABP),∠BAP+∠ABP=
(∠CAB+∠CBA)=
(180°-∠α),据此求解.
(2)根据三角形内角和定理可得∠APB=180°-(∠BAP+∠ABP),∠BAP+∠ABP=
| 1 |
| 2 |
| 1 |
| 2 |
解答: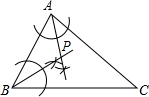 解:(1)如图;
解:(1)如图;
(2)∵∠ACB=α°,
∴∠CAB+∠CBA=180°-∠α,
∴∠BAP+∠ABP=
(∠CAB+∠CBA)=90°-
∠α,
∴∠APB=180°-(∠BAP+∠ABP)=90°+
∠α.
故答案为:90°+
∠α.
 解:(1)如图;
解:(1)如图;(2)∵∠ACB=α°,
∴∠CAB+∠CBA=180°-∠α,
∴∠BAP+∠ABP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠APB=180°-(∠BAP+∠ABP)=90°+
| 1 |
| 2 |
故答案为:90°+
| 1 |
| 2 |
点评:此题主要考查角平分线的作法和定义,以及三角形内角和定理,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 15、第十届亚运会在广东召开,有三名运动员分别住在A、B、C三栋楼,这三栋楼由三条道路相连,如图所示.
15、第十届亚运会在广东召开,有三名运动员分别住在A、B、C三栋楼,这三栋楼由三条道路相连,如图所示. 第十届亚运会在广东召开,有三名运动员分别下榻在A、B、C三个宾馆,三个宾馆由三条道路相连,如图所示.(1)为建一个公共活动场地P到三条道路的距离相等.请用尺方法作出点P,使得点P落在△ABC内部.保留作图痕迹.不要求写作法.(2)如果∠ACB=α°,那么∠APB=______.
第十届亚运会在广东召开,有三名运动员分别下榻在A、B、C三个宾馆,三个宾馆由三条道路相连,如图所示.(1)为建一个公共活动场地P到三条道路的距离相等.请用尺方法作出点P,使得点P落在△ABC内部.保留作图痕迹.不要求写作法.(2)如果∠ACB=α°,那么∠APB=______. 道路相连,如图所示.
道路相连,如图所示.