题目内容
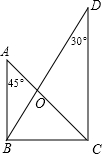如图将一副直角三角板如图叠放，则△AOB与△COD的周长比为1﹕
| 3 |
1﹕
．| 3 |
分析：首先设BC=x，由直角三角形的性质，可求得AB与CD的长，继而求得其比值，易证得△AOB∽△COD，然后由相似三角形的周长比等于相似比，即可求得答案．
解答：解：设BC=x，
∵△ABC是等腰直角三角形，且∠ABC=90°，
∴AB=BC=x，
在Rt△BCD中，∠D=30°，
∴CD=
=
x，
∴AB：CD=1：
，
∵∠ABC∠DCB=90°，
即AB⊥BC，DC⊥BC，
∴AB∥CD，
∴△AOB∽△COD，
∴△AOB与△COD的周长比为：1：
．
故答案为：1：
．
∵△ABC是等腰直角三角形，且∠ABC=90°，
∴AB=BC=x，
在Rt△BCD中，∠D=30°，
∴CD=
| BC |
| tan30° |
| 3 |
∴AB：CD=1：
| 3 |
∵∠ABC∠DCB=90°，
即AB⊥BC，DC⊥BC，
∴AB∥CD，
∴△AOB∽△COD，
∴△AOB与△COD的周长比为：1：
| 3 |
故答案为：1：
| 3 |
点评：此题考查了相似三角形的判定与性质以及解直角三角形的知识．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
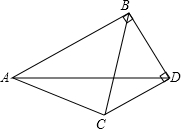将一副直角三角板中的两块按如图摆放，连AD，则tan∠DAC的值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
12、将一副直角三角板如图放置，使含30°角的三角板的段直角边和含45°角的三角板的一条直角边重合，则∠1的度数为
如图将一副直角三角板如图叠放，则△AOB与△COD的周长比为________．