题目内容
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣(k+1)x+k与x轴相交于A、B两点(点B位于点A的左侧),与y轴相交于点C.
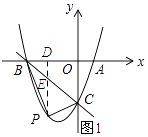
(1)如图1,若k=2,直接写出AB的长:AB= . 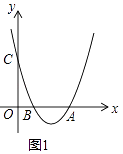
(2)若AB=2,则k的值为 .
(3)如图2,若k=﹣3,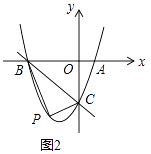
①求直线BC的解析式;
(4)如图3,若k<0,且△ABC是等腰三角形,求k的值.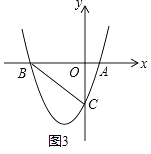
【答案】
(1)1
(2)﹣1或3
(3)
当k=﹣3时,y=x2+2x﹣3,
令x=0得:y=﹣3,令y=0得:x2+2x﹣3=0,解得:x=﹣3或x=1,
∴A(1,0)、B(﹣3,0)、C(0,﹣3).
设直线BC的解析式的y=kx+b,将点B和点C的解析式代入得: ![]() ,解得:k=﹣1,b=﹣3
,解得:k=﹣1,b=﹣3
②点P是直线BC下方抛物线上的一个动点,试求△PBC的面积的最大值及此时点P的坐标
如图1所示:过点P作PD⊥x轴,垂足为D,PD交直线BC与点E.
设P(x,x2+2x﹣3),则点E(x,﹣x﹣3).
∴PE=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2+3x.
∴△BCP的面积=△PEB的面积+△PEC的面积= ![]() PEBD+
PEBD+ ![]() PEOD=
PEOD= ![]() PEOB=
PEOB= ![]() ×3×(﹣x2+3x)=﹣
×3×(﹣x2+3x)=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() .
.
∴当x=﹣ ![]() 时,△PBC的面积取得最大值,最大面积为
时,△PBC的面积取得最大值,最大面积为 ![]() ,此时点P的坐标为(﹣
,此时点P的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )
)
(4)
∵y=x2﹣(k+1)x+k=(x﹣1)(x﹣k),k<0,
∴A(1,0),B(k,0)、C(0,k).
∴OA=1,OB=OC=﹣k.
∴AB=1﹣k,BC=﹣ ![]() k,AC=
k,AC= ![]() .
.
当AB=BC时,有1﹣k=﹣ ![]() k,解得:k=﹣
k,解得:k=﹣ ![]() ﹣1.
﹣1.
当AB=AC时,有1﹣k= ![]() ,解得k=0(舍去),
,解得k=0(舍去),
当BC=AC时,有﹣ ![]() k=
k= ![]() ,整理得:k2=1,解得:k=﹣1或k=1(舍去).
,整理得:k2=1,解得:k=﹣1或k=1(舍去).
综上所述,△ABC是等腰三角形时,k的值为﹣ ![]() ﹣1或﹣1
﹣1或﹣1
【解析】解:(1.)把k=2代入得:y=x2﹣3x+2,
令y=0得:x2﹣3x+2=0,
解得x=2或x=1,
∴A(2,0),B(1,0).
∴AB=1.
所以答案是:1.
(2.)令y=0得:x2﹣(k+1)x+k=0,则(x﹣1)(x﹣k)=0,
解得x=1或x=k.
当点A的坐标为(1,0)时.
∵AB=2,
∴B(﹣1,0).
∴k=﹣1.
当点B的坐标为(1,0)时,
∵AB=2,
∴B(3,0).
∴k=3.
∴k的值为﹣1或3.
所以答案是:﹣1或3
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).

 阅读快车系列答案
阅读快车系列答案